题目内容
若a，b互为相反数，c，d互为倒数，m的绝对值等于4，求
-cd+|m|的值．
| a+b |
| 5 |
考点：代数式求值,相反数,绝对值,倒数
专题：
分析：根据互为相反数的两个数的和等于0可得a+b=0，互为倒数的两个数的乘积是1可得cd=1，根据绝对值的性质求出|m|=4，然后代入代数式进行计算即可得解．
解答：解：∵a，b互为相反数，c，d互为倒数，m的绝对值等于4，
∴a+b=0，cd=1，|m|=4，
∴
-cd+|m|
=0-1+4
=3．
∴a+b=0，cd=1，|m|=4，
∴
| a+b |
| 5 |
=0-1+4
=3．
点评：本题考查了代数式求值，主要利用了相反数的定义，绝对值的性质，倒数的定义，熟记概念与性质是解题的关键，要注意整体思想的利用．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
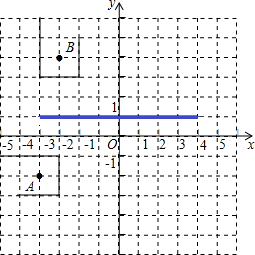如图，机械手要将一个工件从图中的A处移动到B处，但是这个工件不能碰到图中的障碍（不包括坐标轴所表示的紫线），试用坐标写出一条机械手在移动中可能要经过的路线（机械手的行走路线均经过格点）
如图已知∠α，根据三角函数的定义求sinα，cosα，tanα．代数式a=
，4xy，
，a，2014，
a2b，-
中，单项式的个数有（ ）
| 1 |
| 2a |
| a+b |
| 3 |
| 1 |
| 2 |
| 3mn |
| 4 |
| A、3个 | B、4个 | C、5个 | D、6个 |
