题目内容
已知△ABC中,AD⊥BC于D,AE为∠A的平分线,且∠B=35°,∠C=65°,则∠DAE的度数为 .
考点:三角形内角和定理
专题:
分析:首先根据三角形的内角和定理和角平分线的定义求出∠EAC的度数,再根据三角形的内角和定理求出∠DAC的度数,进而求∠DAE的度数.
解答: 解:∵∠B=35°,∠C=65°,
解:∵∠B=35°,∠C=65°,
∴∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
∵AE为∠BAC的平分线,
∴∠EAC=
∠BAC=
×80°=40°.
∵AD⊥BC,
∴∠ADC=90°,
在△ADC中,
∵∠DAC=180°-∠ADC-∠C=180°-90°-65°=25°,
∴∠DAE=∠EAC-∠DAC=40°-25°=15°.
故答案为:15°.
 解:∵∠B=35°,∠C=65°,
解:∵∠B=35°,∠C=65°,∴∠BAC=180°-∠B-∠C=180°-35°-65°=80°.
∵AE为∠BAC的平分线,
∴∠EAC=
| 1 |
| 2 |
| 1 |
| 2 |
∵AD⊥BC,
∴∠ADC=90°,
在△ADC中,
∵∠DAC=180°-∠ADC-∠C=180°-90°-65°=25°,
∴∠DAE=∠EAC-∠DAC=40°-25°=15°.
故答案为:15°.
点评:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
在△ABC中,若三边BC、CA、AB满足BC:CA:AB=5:12:13,则cosB=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,是某宾馆楼梯示意图(一楼至二楼),若要将此楼梯铺上地毯,则至少需要
如图,是某宾馆楼梯示意图(一楼至二楼),若要将此楼梯铺上地毯,则至少需要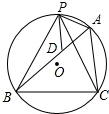 如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧
如图,△ABC内接于⊙O,AB=8,AC=6,D是AB边上的一点,P是优弧
 如图,已知直线y=kx-3经过点M(-2,1),求此直线与x轴,y轴的交点坐标.
如图,已知直线y=kx-3经过点M(-2,1),求此直线与x轴,y轴的交点坐标.