题目内容
如图所示，已知AD是直角三角形ABC斜边上的高，BE平分∠B交AD于G，AC于E，过E作EF⊥BC于F．
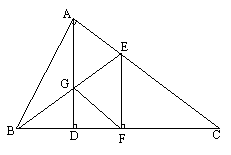
(1)AG与AE相等吗？试说明理由；
(2)四边形AEFG是菱形吗？试说明理由．
答案：
解析：
解析：
|
解：(1)AG与AE相等 ∠EBD＋∠BGD＝∠ABE＋∠AEB＝ 而∠ABE＝∠EBD 所以∠BGD＝∠AEB＝∠AGE 可以得到AG＝AE (2)由△ABE与△FBE是关于直线BE轴对称，可以得到AG＝GF＝AE＝EF且AG∥EF，所以四边形AGFE是菱形． |
练习册系列答案
相关题目
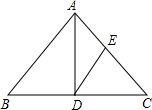如图所示，已知AD是等腰△ABC底边上的高，且tan∠B=| 3 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
23、如图所示，已知AD是△ABC的角平分线，DE⊥AB，DF⊥AC，垂足分别为E，F．试说明：AD垂直平分EF．
17、如图所示，已知AD是△ABC的角平分线，DE∥AC交AB于点E，DF∥AB交AC于点F，
如图所示，已知AD是△ABC的中线，在AD及延长线上截取DE=DF，连接CE，BF．