题目内容
等腰三角形的一腰长为6cm,底边长为6
cm,请你判断这个是 (填“锐角”、“直角”、“钝角”)三角形,它的三个角分别是多少?
| 3 |
考点:解直角三角形,等腰三角形的性质
专题:
分析:根据等腰三角形的性质求得等腰三角形的底边上的高的长,然后求得两个底角的度数,从而求得顶角的度数,得到该三角形的形状.
解答: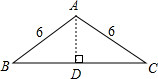 解:如图:由题意得:AB=AC=6cm,BC=6
解:如图:由题意得:AB=AC=6cm,BC=6
cm,
作AD⊥BC于点D,
则BD=DC=3
cm,
由勾股定理得:AD=
=
=3=
AB,
∴∠B=∠C=30°,
∴∠BAC=120°,
∴该三角形是钝角三角形,
所以该三角形是钝角三角形,它的三个角分别是30°,30°,120°.
故答案为:钝角.
 解:如图:由题意得:AB=AC=6cm,BC=6
解:如图:由题意得:AB=AC=6cm,BC=6| 3 |
作AD⊥BC于点D,
则BD=DC=3
| 3 |
由勾股定理得:AD=
| AB2-BD2 |
62-(3
|
| 1 |
| 2 |
∴∠B=∠C=30°,
∴∠BAC=120°,
∴该三角形是钝角三角形,
所以该三角形是钝角三角形,它的三个角分别是30°,30°,120°.
故答案为:钝角.
点评:本题考查了解直角三角形,等腰三角形的性质,解题的关键是构造直角三角形并求得底边上的高的长度.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
已知扇形的圆心角为120°,半径为6cm,则扇形的面积为( )
| A、12cm2 |
| B、36cm2 |
| C、12πcm2 |
| D、36πcm2 |
下列函数中是二次函数的是( )
| A、y=4x2+1 | ||
| B、y=4x+1 | ||
C、y=
| ||
D、y=
|
已知⊙O的半径为2,圆心O到直线l的距离PO=1,则直线l与⊙O的位置关系是( )
| A、相切 | B、相离 |
| C、相交 | D、无法判断 |
 如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )
如图,∠A=∠B=90°,AB=7,AD=2,BC=3,在边AB上取点P,使得△PAD与△PBC相似,则这样的P点共有( )| A、1个 | B、2个 | C、3个 | D、4个 |
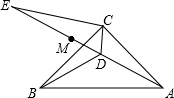 如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.
如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,∠CAD=∠CBD=15°,E为AD延长线上的一点,且CE=CA.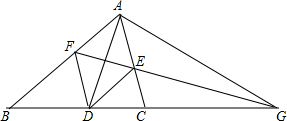 如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证:
如图,AD是∠BAC的平分线,DE平行AB交AC于点E,DF平行AC交AB于点F,延长FE交BC的延长线于点G,求证: 在平行四边形ABCD中,AB:AD=3:2,∠ADB=60°,求sinA的值.
在平行四边形ABCD中,AB:AD=3:2,∠ADB=60°,求sinA的值.