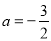题目内容
在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+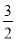 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
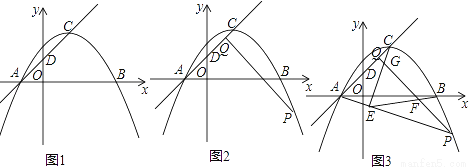
(1)如图1,求抛物线的顶点坐标;
(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;
(3)在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
(1)C(1,2);(2)m=﹣t2+t+;(3)P(,﹣) 【解析】试题分析:(1)先由抛物线解析式确定出对称轴,再用中点坐标确定出点A的坐标,代入抛物线解析式确定出抛物线解析式,化为顶点式即可得出顶点坐标; (2)由(1)的条件,确定出直线AC解析式,由PQ⊥AC,确定出点P的坐标,消去y即可; (3)先判断出△ACE∽△APQ,再判断出∠ACB=90°,从而得到Rt△BCD...
练习册系列答案
相关题目

 B.
B.  C.
C.  D.
D. 
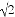 ,则图中阴影部分的面积是___________
,则图中阴影部分的面积是___________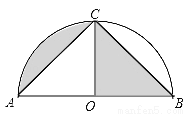
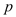 的所有可能值是_________________;
的所有可能值是_________________;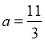 B. a=1 C.
B. a=1 C. 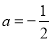 D.
D.