题目内容
20.已知圆内接平行四边形的一边为$\sqrt{6}$,面积为3$\sqrt{2}$.则该圆的面积为$\frac{9}{4}$π.分析 根据圆内接四边形的性质和平行四边形的性质证明四边形ABCD是矩形,根据矩形的面积公式求出另一边长,根据勾股定理求出圆的直径,计算即可.
解答 解:连接AC ,
,
∵四边形ABCD是平行四边形,
∴∠BAC+∠B=180°,∴∠BAC+∠D=180°,
∴∠B=∠D,
∵四边形ABCD是圆内接平行四边形,
∴∠B+∠D=180°,
∴∠B=∠D=90°,
∴四边形ABCD是矩形,
∵四边形ABCD的一边AD=$\sqrt{6}$,面积为3$\sqrt{2}$,
∴AB=$\sqrt{3}$,
∴AC=3,
∴该圆的面积为$\frac{9}{4}$π,
故答案为:$\frac{9}{4}$π.
点评 本题考查的是圆内接四边形的性质、平行四边形的性质,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
11.某商店以每套80元的进价购进8套服装,并以90元左右的价格卖出.如果以90元为标准,超过标准的售价记为正数,不足标准的售价记为负数,出售价格记录如下:+2,-3,+5,+1,-2,-1,0,-5(单位:元).其它收支不计,当商店卖完这8套服装后( )
| A. | 盈利 | B. | 亏损 | C. | 不盈不亏 | D. | 盈亏不明 |
12.以下列各组长度的线段为边,能构成三角形的是( )
| A. | 3cm、4cm、8cm | B. | 5cm、5cm、11cm | C. | 12cm、5cm、6cm | D. | 8cm、6cm、4cm |
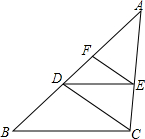 已知:如图,在△ABC中,DE∥BC,EF∥CD.
已知:如图,在△ABC中,DE∥BC,EF∥CD.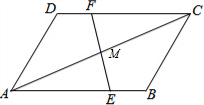 如图,AB∥CD,AD∥BC,E,F分别在AB,CD上,DF=BE,AC与EF相交于点M.求证:AC、EF互相平分.
如图,AB∥CD,AD∥BC,E,F分别在AB,CD上,DF=BE,AC与EF相交于点M.求证:AC、EF互相平分.