题目内容
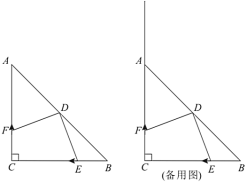
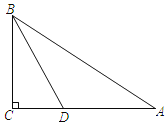
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 延长线上一点,连接
延长线上一点,连接![]() ,过点
,过点![]() 作
作![]() 于
于![]() .
.
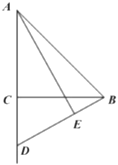
(1)求证:![]() .
.
(2)将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后,所得的射线与线段
后,所得的射线与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.
①依题意补全图形;
②用等式表示线段![]() ,
,![]() ,
,![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)详见解析;(2)①详见解析;②![]() ,理由详见解析.
,理由详见解析.
【解析】
(1)利用同角的余角即可解出此问.
(2)①根据题意补全图形;②过点C作CG⊥CE角AE于G,进而判断出∠CAE=∠CBD,即可判断△ACG≌△BCE,得出AG=BE,CG=CE,进而判断出EC=![]() CE,得出AE=BE+
CE,得出AE=BE+![]() CE,再判断出EF=AE,即可.
CE,再判断出EF=AE,即可.
(1)证明:如图1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
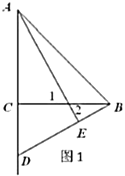
(2)①补全图形如图2.

②![]() .
.
证明:在![]() 上截取
上截取![]() ,使
,使![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
又∵![]() .
.
∴![]() .
.
∴![]() .
.
又∵射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]()
后得到![]() ,且
,且![]() ,
,
∴![]() .
.
∴![]()

练习册系列答案
相关题目