题目内容
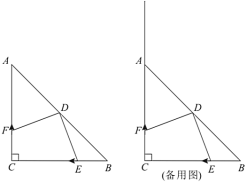
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
【答案】(1)8;(2)见解析;(3)![]() 或4或
或4或![]() 或
或![]() .
.
【解析】
(1)直接可求△ABC的面积;
(2)连接CD,根据等腰直角三角形的性质可求:∠A=∠B=∠ACD=∠DCB=45°,即BD=CD,且BE=CF,即可证△CDF≌△BDE,可得DE=DF;
(3)分△ADF的面积是△BDE的面积的两倍和△BDE与△ADF的面积的2倍两种情况讨论,根据题意列出方程可求x的值.
解:(1)∵S△ABC=![]()
![]() AC×BC
AC×BC
∴S△ABC=![]() ×4×4=8(cm2)
×4×4=8(cm2)
故答案为:8
(2)如图:连接CD
∵AC=BC,D是AB中点
∴CD平分∠ACB
又∵∠ACB=90°
∴∠A=∠B=∠ACD=∠DCB=45°
∴CD=BD
依题意得:BE=CF
∴在△CDF与△BDE中
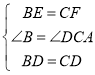
∴△CDF≌△BDE(SAS)
∴DE=DF
(3)如图:过点D作DM⊥BC于点M,DN⊥AC于点N,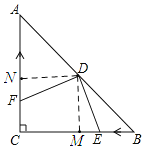
∵AD=BD,∠A=∠B=45°,∠AND=∠DMB=90°
∴△ADN≌△BDM(AAS)
∴DN=DM
若S△ADF=2S△BDE.
∴![]() ×AF×DN=2×
×AF×DN=2×![]() ×BE×DM
×BE×DM
∴|4-3x|=2x
∴x1=4,x2=![]()
若2S△ADF=S△BDE
∴2×![]() ×AF×DN=
×AF×DN=![]() ×BE×DM
×BE×DM
∴2×|4-3x|=x
∴x1=![]() ,x2=
,x2=![]()
综上所述:x=![]() 或4或
或4或![]() 或
或![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目