Question

2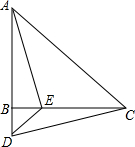．如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．求证：△ABE≌△CBD．

Answer 1

分析 根据已知条件利用SAS即可．

解答 证明：∵∠ABC=90°，D为AB延长线上一点，
∴∠ABE=∠CBD=90°，
在△ABE和△CBD中，
$\left\{\begin{array}{l}{AB=CB}\\{∠ABE=∠CBD}\\{BE=BD}\end{array}\right.$，
∴△ABE≌△CBD（SAS）．

点评 此题主要考查了全等三角形的判定，熟练掌握全等三角形的判定是解本题的关键．