题目内容
16.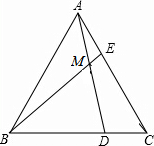 如图,在等边△ABC中,点D,E分别在BC,AC上,DC=EA,AD与BE交于点M,那么∠AMB=120°.
如图,在等边△ABC中,点D,E分别在BC,AC上,DC=EA,AD与BE交于点M,那么∠AMB=120°.
分析 根据等边三角形的性质得到AB=AC,∠BAE=∠C=60°,推出△ABE≌△ACD,根据全等三角形的性质得到∠AEB=∠ADC,然后根据外角的性质即可得到结论.
解答 解:在等边△ABC中,
∵AB=AC,∠BAE=∠C=60°,
在△ABE与△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠C}\\{AE=CD}\end{array}\right.$,
∴△ABE≌△ACD,
∴∠AEB=∠ADC,
∵∠AMB=∠MAE+∠AEB=∠MAE+∠ADC=180°-∠C=120°.
故答案为:120°.
点评 本题考查了全等三角形的判定和性质,关键是根据等边三角形的性质:等边三角形的三个内角都相等,且都等于60°;三条边相等.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
7.2015年4月17日河北新闻报道,一季度全省全部财政收入累计完成1063.7亿元,比2014年同期增长6.7%(增长率=$\frac{2015年一季度全部财政收入-2014年一季度全部财政收入}{2014年一季度全部财政收入}$),则2014年一季度全省全部财政收入累计完成(结果精确到十分位)( )
| A. | 996.9亿元 | B. | 996.90亿元 | C. | 997.0亿元 | D. | 996.91亿元 |
4.已知一个多项式与2x2-3x-2的和等于x2-2x-3,则这个多项式是( )
| A. | -x2+2x+1 | B. | -x2+x-1 | C. | x2-x+1 | D. | -x2+x+1 |