题目内容
5.把下列各式进行因式分解:(1)8x3-8x2-4x;
(2)6x3y(x-y)3-4xy3(y-x)2;
(3)x(m-n)2-y(n-m)2;
(4)2m3n-6m2n+mn.
分析 (1)原式提取公因式即可得到结果;
(2)原式变形后,提取公因式即可得到结果;
(3)原式变形后,提取公因式即可得到结果;
(4)原式提取公因式即可得到结果.
解答 解:(1)8x3-8x2-4x=4x(2x2-2x-1);
(2)6x3y(x-y)3-4xy3(y-x)2=6x3y(x-y)3-4xy3(x-y)2=2xy(x-y)2[3x2(x-y)-2y2];
(3)x(m-n)2-y(n-m)2=x(m-n)2-y(m-n)2=(x-y)(m-n)2;
(4)2m3n-6m2n+mn=mn(2m2n-6mn+1).
点评 此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
15.下列三根小木棒,把它们首尾顺次相接能摆成一个三角形的是( )
| A. | 1,1,3 | B. | 5,6,7 | C. | 1,8,18 | D. | 3,4,10 |
17.把-4x3+8x2+16x因式分解的结果是( )
| A. | -x(4x2-8x+16) | B. | x(-4x2+8x-16) | C. | 4(-x3+2x2-4x) | D. | -4x(x2-2x-4) |
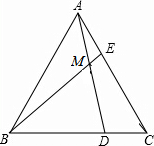 如图,在等边△ABC中,点D,E分别在BC,AC上,DC=EA,AD与BE交于点M,那么∠AMB=120°.
如图,在等边△ABC中,点D,E分别在BC,AC上,DC=EA,AD与BE交于点M,那么∠AMB=120°. 如图,OD平分∠COA,OE平分∠COB,那么∠EOD等于多少度?你能找到图中互余的角有哪些?互补的角有哪些?
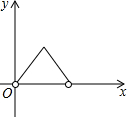
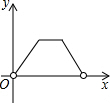
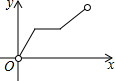
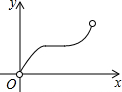
如图,OD平分∠COA,OE平分∠COB,那么∠EOD等于多少度?你能找到图中互余的角有哪些?互补的角有哪些?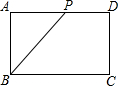 如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )
如图,点P是长方形ABCD边上一动点,沿A→D→C→B的路径移动,设P点经过的路径长为x,△BAP的面积是y,则下列能大致反映y与x的函数关系的图象是( )