题目内容
 如图,点P为双曲线y=-
如图,点P为双曲线y=-| 4 |
| x |
| k |
| x |
-1
-1
.分析:利用反比例函数系数k的几何意义得出PC×PD=4,S△OCB+S△ADO=|xy|=|k|=4-3=1,即可得出k的值.
解答: 解:延长PB到y轴于点C,延长PA到x轴于点D,
解:延长PB到y轴于点C,延长PA到x轴于点D,
∵点P为双曲线y=-
(x<0)上一点,PA∥y 轴,PB∥x 轴,
∴PC×PD=4,
∵双曲线y=
(x<0)于A、B两点,且S四边形PAOB=3,
∴S△OCB+S△ADO=|xy|=|k|=4-3=1,
∴k=-1,
故答案为:-1.
 解:延长PB到y轴于点C,延长PA到x轴于点D,
解:延长PB到y轴于点C,延长PA到x轴于点D,∵点P为双曲线y=-
| 4 |
| x |
∴PC×PD=4,
∵双曲线y=
| k |
| x |
∴S△OCB+S△ADO=|xy|=|k|=4-3=1,
∴k=-1,
故答案为:-1.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出图形之间的面积关系是解题关键.

练习册系列答案
相关题目
 如图,点A为双曲线y=
如图,点A为双曲线y=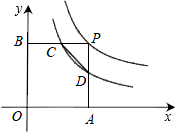 如图,点P为双曲线
如图,点P为双曲线 如图,点A为双曲线
如图,点A为双曲线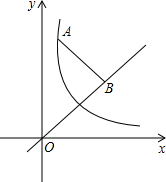 如图,点A为双曲线
如图,点A为双曲线 如图、点A为双曲线上一点,AB⊥x轴,SOAB=3,则双曲线的解析式为( )
如图、点A为双曲线上一点,AB⊥x轴,SOAB=3,则双曲线的解析式为( )