Question

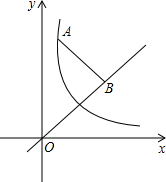如图，点A为双曲线y=

k

x

的图象上一点，点B是直线y=x的图象上一点，且AB⊥OB，若OB²-AB²=5，则k=

5

2

．

Answer 1

分析：首先过点A作AD∥x轴，交直线OB于点D，作AC∥y轴，交直线OB于点C，易得△ABD与△ABC是等腰直角三角形，即AB=AD=BC，又由OB²-AB²=5，可得OD•OC=5，设点A的坐标为：（x，

k

x

），可得点C的坐标为：（x，x），点D的坐标为：（

k

x

，

k

x

），则OC=

2

x，OD=

2 k

x

，即可得方程：

2

x•

2 k

x

=5，解此方程即可求得答案．

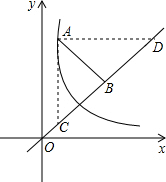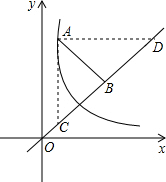解答：解：过点A作AD∥x轴，交直线OB于点D，作AC∥y轴，交直线OB于点C，
∵直线OB的解析式为：y=x，
∴∠xOB=∠BOy=45°，
∴∠ADB=∠ACB=45°
∵AB⊥OB，
∴△ABD与△ABC是等腰直角三角形，
∴AB=AD=BC，
∵OB²-AB²=5，
∴（OB+AB）（OB-AB）=5，
即（OB+BD）（OB-BC）=OD•OC=5，
设点A的坐标为：（x，

k

x

），
∴点C的坐标为：（x，x），点D的坐标为：（

k

x

，

k

x

），
∴OC=

2

x，OD=

2 k

x

，
∴

2

x•

2 k

x

=5，
解得：k=

5

2

．
故答案为：

5

2

．

点评：此题考查了反比函数与一次函数的性质、平方差公式以及等腰直角三角形性质．此题难度较大，解题的关键是辅助线的构造，注意掌握数形结合思想与方程思想的应用．