题目内容
如图，点A为双曲线y=| k | x |
分析：由△AOB为等腰直角三角形可知点A纵横坐标相同，且在直线y=3x-4上，所以可求点A坐标（2，2），由此即可求出k．
解答：
解：如图，过A作AC⊥OB于C，
∵△AOB为等腰直角三角形，
∴AC=OC，
∴点A纵横坐标相同，
又在直线y=3x-4上，
∴点A坐标（2，2），
∵又在双曲线y=
（x＞0）上，
∴k=2×2=4．
故填空答案：4．
解：如图，过A作AC⊥OB于C，∵△AOB为等腰直角三角形，
∴AC=OC，
∴点A纵横坐标相同，
又在直线y=3x-4上，
∴点A坐标（2，2），
∵又在双曲线y=
| k |
| x |
∴k=2×2=4．
故填空答案：4．
点评：此题难度稍大，主要考查反比例函数图象和性质、等腰直角三角形性质及用坐标表示线段长．
练习册系列答案
相关题目
如图，点P为双曲线
如图，点A为双曲线
如图，点A为双曲线
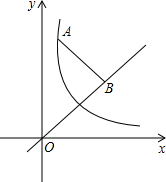如图、点A为双曲线上一点，AB⊥x轴，SOAB=3，则双曲线的解析式为（ ）