��Ŀ����
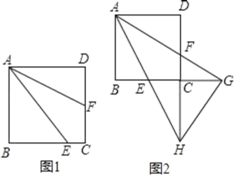
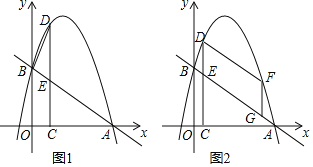
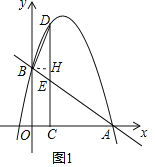
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���y����![]() x+3��ͼ����x�ύ�ڵ�A����y�ύ��B�㣬������y����x2+bx+c����A��B���㣬�ڵ�һ������������ȡһ��D������D��DC��x���ڵ�C����ֱ��AB�ڵ�E��
x+3��ͼ����x�ύ�ڵ�A����y�ύ��B�㣬������y����x2+bx+c����A��B���㣬�ڵ�һ������������ȡһ��D������D��DC��x���ڵ�C����ֱ��AB�ڵ�E��
��1���������ߵĺ�������ʽ
��2���Ƿ���ڵ�D��ʹ����BDE����ACE���ƣ������ڣ��������D�����꣬�������ڣ���˵�����ɣ�
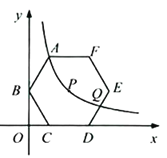
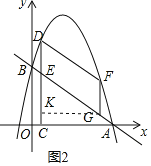
��3����ͼ2��F�ǵ�һ�������������ϵĶ��㣨�����D�غϣ�����G���߶�AB�ϵĶ��㣮����DF��FG�����ı���DEGF��ƽ���ı������ܳ����ʱ����ֱ��д����G�����꣮
���𰸡���1��y����x2+![]() x+3����2�����ڣ���D������Ϊ��
x+3����2�����ڣ���D������Ϊ��![]() ��3����
��3����![]() ��
��![]() ������3��G��
������3��G��![]() ��
��![]() ����
����
��������
��1������![]() �����A��B�����꣬�ٴ��������߽���ʽ�м�����������߽���ʽ��
�����A��B�����꣬�ٴ��������߽���ʽ�м�����������߽���ʽ��
��2����BDE����ACE���ƣ�Ҫ����������������ۣ��١�BDE�ס�ACE�����![]() ��
��![]()
���ڡ�DBE�ס�ACE�����![]() ��
��![]() ��
��
��3����DEGF��ƽ���ı��Σ��ɵ�DE��FG��DE=FG����![]() ��
��![]() ��
��![]() ��
��![]() ������ƽ���ı����ܳ���ʽ�ɵã�DEGF�ܳ�=
������ƽ���ı����ܳ���ʽ�ɵã�DEGF�ܳ�=![]() ���ɴ˿���õ�G�����꣮
���ɴ˿���õ�G�����꣮
�⣺��1����![]() �У���
����![]() ����
����![]() ����
����![]() ����
����![]() ��
��
![]() ��
��![]() ��
��
��![]() ��
��![]() �ֱ����������
�ֱ����������![]() �У��ã�
�У��ã�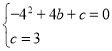 ����ã�
����ã�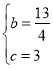 ��
��
![]() �����ߵĺ�������ʽΪ��
�����ߵĺ�������ʽΪ��![]() ��
��
��2�����ڣ���ͼ1������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ��
��![]() ���ƣ�
���ƣ�![]()
![]() ��
��![]()
�ٵ�![]() ʱ��
ʱ��![]() ��
��
![]()
![]() ������
������![]()
![]() ����ã�
����ã�![]() ����ȥ����
����ȥ����![]() ����ȥ����
����ȥ����![]() ��
��
![]() ��
��![]()
�ڵ�![]() ʱ��
ʱ��![]()
![]()
![]() ��
��
![]()
![]() ������
������![]()
![]() ����ã�
����ã�![]() ����
����![]() ��
��![]() ����
����![]() ��
��![]() ��
��
![]() ��
��![]() ��
��
������������![]() ������Ϊ
������Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��
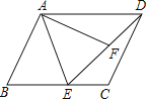
��3����ͼ3��![]() �ı���
�ı���![]() ��ƽ���ı���
��ƽ���ı���
![]() ��
��![]()
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
![]() ������
������![]() ��
��![]()
![]() ������
������![]()
����![]() ��
��![]() ��
��![]() ����
����![]()
![]()
![]()
![]() ������
������![]()
![]() ������
������![]()
![]() �ܳ�
�ܳ�![]()
![]() ��
��
![]() ��
��![]() ʱ��
ʱ��![]() �ܳ����ֵ
�ܳ����ֵ![]() ��
��
![]() ��
��![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ij����ѧ��ȤС��Ժ���![]() ��ͼ������ʽ�������̽����̽���������£��벹��������
��ͼ������ʽ�������̽����̽���������£��벹��������
��1���Ա���![]() ��ȡֵ��Χ�dz�0���ȫ��ʵ����
��ȡֵ��Χ�dz�0���ȫ��ʵ����![]() ��
��![]() �ļ����Ӧֵ�б����£�
�ļ����Ӧֵ�б����£�
| �� |
|
|
|
| 1 | 2 | 3 | 6 | �� |
| �� | 1 | 2 |
| 6 | 1 | 3 | 2 | 1 | �� |
����![]() _________��
_________��
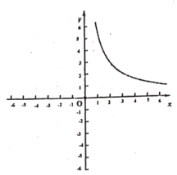
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㲢�����˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
��3���۲캯��ͼ��д��һ���������ʣ�
��4����һ��̽������ͼ���֣�
�ٺ���ͼ����![]() �ύ�������________�����Զ�Ӧ����
�ύ�������________�����Զ�Ӧ����![]() ��ʵ�����������________��
��ʵ�����������________��
�ڷ���![]() ��_______��ʵЧ����
��_______��ʵЧ����
�۹���![]() �ķ���
�ķ���![]() ��2��ʵ������
��2��ʵ������![]() ��ȡֵ��Χ��________��
��ȡֵ��Χ��________��