题目内容
【题目】如图，已知等边
的边长为8，点P是AB边上的一个动点(与点A、B不重合)，直线
是经过点P的一条直线，把沿直线折叠，点B的对应点是点
.
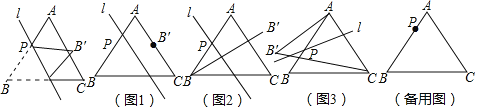
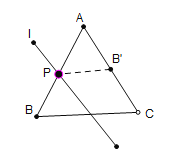
(1)如图1，当
时，若点恰好在AC边上，则
的长度为 ；
(2)如图2，当
时，若直线
，则
的长度为 ；
(3)如图3，点P在AB边上运动过程中，若直线始终垂直于AC，
的面积是否变化？若变化，说明理由；若不变化，求出面积；
(4)当
时，在直线变化过程中，求面积的最大值.
【答案】（1）长度为4；（2）长度为5
；（3）△
的面积不变化为16，理由见解析；（4）△的面积的最大值为24+4，理由见解析.
【解析】
（1）连接
，由于折叠则△
为等边三角形，即可求出
的长度；（2）记
与BC交于点D，连接和
，△BPD和△
为边长等于5的等边三角形，所以
为两边长为5的等边三角形的高之和，求出即可；（3）因为⊥AC， ∥，则
到AC的距离始终等于B到AC的距离（平行线之间的距离处处相等），
的面积和△ABC的面积相等，算出即可；（4）由题意知=PB=6,所以始终在以P点为圆心，6为半径的圆上运动，要使得△
面积最大，只要AC边上的高
最大，如图，当经过圆心P时，最大，算出其面积即可.
（1）连接，
∵等边
的边长为8，PB=4，
∴AP==4，∠PAC=60°，
∴△为等边三角形，
∴=4；
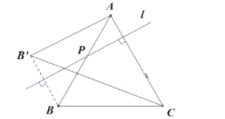
（2）记与BC交于点D，连接和，
∵∥BC，=BP=5，
∴△BPD为边长等于5的等边三角形，
所以PD==5，∠=∠BPD=60°，
∴△为边长等于5的等边三角形，
由折叠知⊥，
∴为两边长为5的等边三角形的高之和，
则=
；
（3）△的面积不变化，理由如下：
∵⊥AC， ∥，
∴到AC的距离始终等于B到AC的距离（平行线之间的距离处处相等），
∴S△ACB’=S△ABC=
×82=
；
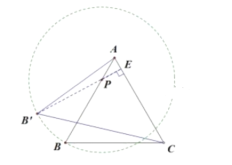
（4）由题意知=PB=6,所以始终在以P点为圆心，6为半径的圆上运动，要使得△面积最大，只要AC边上的高最大，如图，当经过圆心P时最大，
∵∠BAC=60°，
∴AE=
AP=1，PE=AE=，=+6，
此时S△ACB’的最大值为×AC×=×8×（+6）=
+24
