题目内容
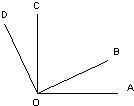
 如图,OA⊥OC,OB⊥OD,若∠BOC=α,则∠AOD的度数为
如图,OA⊥OC,OB⊥OD,若∠BOC=α,则∠AOD的度数为
- A.180°-2a
- B.180°-a
- C.

- D.2a-90°
B
分析:首先根据垂直定义可得∠DOB=90°,∠AOC=90°,再根据∠BOC=α,可得∠COD=90°-α,然后再由∠AOD=∠AOC+∠DOC可得答案.
解答:∵0A⊥OC,OB⊥OD,
∴∠DOB=90°,∠AOC=90°,
∵∠BOC=α,
∴∠COD=90°-α,
∴∠AOD=∠AOC+∠DOC=90°+90°-α=180°-α,
故选:B.
点评:此题主要考查了垂线,关键是掌握两直线互相垂直式时,夹角为90°.
分析:首先根据垂直定义可得∠DOB=90°,∠AOC=90°,再根据∠BOC=α,可得∠COD=90°-α,然后再由∠AOD=∠AOC+∠DOC可得答案.
解答:∵0A⊥OC,OB⊥OD,
∴∠DOB=90°,∠AOC=90°,
∵∠BOC=α,
∴∠COD=90°-α,
∴∠AOD=∠AOC+∠DOC=90°+90°-α=180°-α,
故选:B.
点评:此题主要考查了垂线,关键是掌握两直线互相垂直式时,夹角为90°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

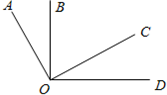 9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( )
9、如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点.甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有5个.其中正确的结论是( ) 已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD.
已知:如图,OA=OC,OB=OD,试说明:△AOB≌△COD. 8、如图,OA=OC,OB=OD,则图中全等三角形共有
8、如图,OA=OC,OB=OD,则图中全等三角形共有 10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=
10、如图,OA⊥OC,OB⊥OD,∠BOC=35°,则∠AOD=