题目内容
如图①,一只蚂蚁从圆锥底面的A点出发,沿侧面绕行一周后到达母线SA的中点M.蚂蚁沿怎样的路径行走最合算?为了解决这一问题,爱动脑筋的银银、慧慧与乐乐展开了研究.(1)善于表现的银银首先列出了一组数据:圆锥底面半径r=10cm,母线SA长为40cm,就这组数据,请你求出蚂蚁所走的最短路程;
(2)一向稳重的慧慧只给出一个数据:圆锥的锥角等于60°(如图②),请问:蚂蚁如何行走最合算?
(3)通过(1)、(2)的计算与归纳,银银、慧慧自认为他们已找到问题的解决方法,可老谋深算的乐乐认为他们考虑欠周,
①请你分析,乐乐为什么认为他们考虑欠周?
②结合上面的研究,请你给出这一问题的一般性解法.

【答案】分析:圆锥展开成平面后是扇形,要路径最短,就要展开后,蚂蚁爬的是直角三角形的一条直角边才可以.
(1)根据条件求出展开的扇形的圆心角度数,然后求结果看看.
(2)根据锥角可找出母线和半径的关系,但都不知道长.
(3)根据求得的数据和不能求解可知道考虑千周,然后给出一般性解法.
解答:解:(1)2π•10=nπ•40÷180°
n=90°,
AM= =20
=20 .
.
(2)∵锥角为60°,
∴底面半径的长和母线的长相等,
但缺少母线的长.
(3)①因为银银的数据不合理,因为慧慧缺少条件.
②(1)展成平面图形.
(2)知道母线的长,知道扇形的圆心角度数,以及M是SA的中点,根据三角函数或者构造直角三角形来求解.
点评:本题考查平面展开最短路径问题,关键知道圆锥展开成平面后是扇形,且爬行的路线是三角形的一边,根据三角形的特点求解.
(1)根据条件求出展开的扇形的圆心角度数,然后求结果看看.
(2)根据锥角可找出母线和半径的关系,但都不知道长.
(3)根据求得的数据和不能求解可知道考虑千周,然后给出一般性解法.
解答:解:(1)2π•10=nπ•40÷180°
n=90°,
AM=
 =20
=20 .
.(2)∵锥角为60°,
∴底面半径的长和母线的长相等,
但缺少母线的长.
(3)①因为银银的数据不合理,因为慧慧缺少条件.
②(1)展成平面图形.
(2)知道母线的长,知道扇形的圆心角度数,以及M是SA的中点,根据三角函数或者构造直角三角形来求解.

点评:本题考查平面展开最短路径问题,关键知道圆锥展开成平面后是扇形,且爬行的路线是三角形的一边,根据三角形的特点求解.

练习册系列答案
相关题目
 已知如图,圆锥的底面圆的半径为r(r>0),母线长OA为3r,C为母线OB的中点在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短线路长为( )
已知如图,圆锥的底面圆的半径为r(r>0),母线长OA为3r,C为母线OB的中点在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短线路长为( )A、
| ||||
B、
| ||||
C、
| ||||
D、3
|
 如图,一圆柱体的底面圆周长为24cm,高AB为4cm,BC是直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C的最短路程是( )
如图,一圆柱体的底面圆周长为24cm,高AB为4cm,BC是直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C的最短路程是( )A、4
| ||
B、4
| ||
C、
| ||
D、π+
|
 如图,一圆柱体的底面圆周长为6cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,则爬行的最短路程为( )
如图,一圆柱体的底面圆周长为6cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,则爬行的最短路程为( )| A、5cm | ||
| B、5πcm | ||
C、2
| ||
D、2
|
 如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为8cm,母线OF长为8cm,在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为( )
如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为8cm,母线OF长为8cm,在母线OF上的点A处有一块爆米花残渣,且FA=2cm,一只蚂蚁从杯口的点E处沿圆锥表面爬行到A点,则此蚂蚁爬行的最短距离为( )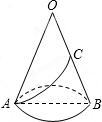 已知如图,圆锥的底面圆的半径为r(r>0),母线长OA为2r,C为母线OB的中点.在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短线路长为
已知如图,圆锥的底面圆的半径为r(r>0),母线长OA为2r,C为母线OB的中点.在圆锥的侧面上,一只蚂蚁从点A爬行到点C的最短线路长为