题目内容
如图，为了测量池塘的宽DE，在岸边找到点C，测得CD=30m，在DC的延长线上找一点A，测得AC=5m，过点A作AB∥DE交EC的延长线于B，测出AB=6m，则池塘的宽DE为（ ）| A、25m | B、30m |
| C、36m | D、40m |
考点：相似三角形的应用
专题：计算题
分析：由AB∥DE可判断△CED∽△CBA，然后了相似比可计算出DE的长．
解答：解：∵AB∥DE，
∴△CED∽△CBA，
∴
=
，即
=
，
∴DE=36（m）．
故选C．
∴△CED∽△CBA，
∴
| DE |
| AB |
| DC |
| AC |
| DE |
| 6 |
| 30 |
| 5 |
∴DE=36（m）．
故选C．
点评：本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度（测量距离）；借助标杆或直尺测量物体的高度．
练习册系列答案
孟建平名校考卷系列答案
相关题目
如图，圆O与四边形ABCD四边都相切，试讨论四边形ABCD边与边之间有何关系．
实数a，b在数轴上表示如图：则下列结论正确的有
有理数a，b在数轴上的位置如图所示，则下列各式的符号为负的是（ ）| A、-a+b |
| B、-ab2 |
| C、-a3b3 |
| D、a3b3 |
如图，在四边形ABCD中，边AB与AD关于AC对称，则下面结论正确的是（ ）①CA平分∠BCD；②AC平分∠BAD；③DB⊥AC；④BE=DE．
| A、② | B、①② |
| C、②③④ | D、①②③④ |
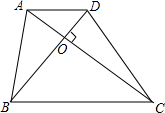如图所示已知梯形ABCD中，AD∥BC，BD=6，AC=8，AC⊥BD于O，