题目内容
8.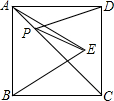 如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6.
如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6.
分析 由于点B与D关于AC对称,所以连接BD,交AC于P点.此时PD+PE的最小值=BE,而BE是等边△ABE的边,BE=AB,由正方形ABCD的边长为6,可求出AB的长,从而得出结果.
解答  解:设BE与AC交于点P,连接BD,
解:设BE与AC交于点P,连接BD,
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的边长为6,
∴AB=6.
又∵△ABE是等边三角形,
∴BE=AB=6.
故所求最小值为6.
故答案为:6.
点评 此题主要考查轴对称--最短路线问题,要灵活运用对称性解决此类问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.下列实数中,无理数是( )
| A. | 0 | B. | $\sqrt{2}$ | C. | -2 | D. | $\frac{2}{7}$ |
1.正比例函数y=kx(k<0),当x1=-3,x2=0,x3=2时,对应的y1,y2,y3之间的关系是( )
| A. | y3<y2,y1<y2 | B. | y1<y2<y3 | C. | y1>y2>y3 | D. | 无法确定 |
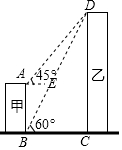 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号) 如图是一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )
如图是一个圆柱体和一个长方体组成的几何体,圆柱的下底面紧贴在长方体的上底面上,那么这个几何体的俯视图为( )



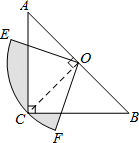 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )