题目内容
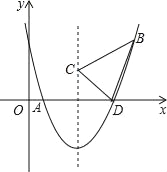
【题目】已知抛物线c:y=-x2-2x+3和直线l:y=![]() x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
(1)当直线l与这个新图象有且只有一个公共点时,d= ;
(2)当直线l与这个新图象有且只有三个公共点时,求d的值;
(3)当直线l与这个新图象有且只有两个公共点时,求d的取值范围;
(4)当直线l与这个新图象有四个公共点时,直接写出d的取值范围.
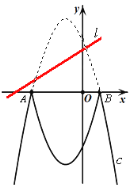
【答案】(1)d=![]() ;(2)d=
;(2)d=![]() 或d=
或d=![]() (3)
(3)![]() <d<
<d<![]() 或d<
或d<![]() ; (4)
; (4)![]() <d<
<d<![]() 。
。
【解析】
(1)令-x2-2x+3=![]() x+d求解即可;
x+d求解即可;
(2)设抛物线c:y=-x2-2x+3与x轴交于点A(-3,0),点B(1,0),则根据方程有两个相等的实根求出P的坐标,然后求解即可;
(3)(4)根据(2)求出的P点坐标进行数形结合画图找出d的取值范围即可.
解:(1)当直线l经过点A(-3,0)时,d=![]() ;
;
(2)设抛物线c:y=-x2-2x+3与x轴交于点A(-3,0),点B(1,0),
直线l:y=![]() x+d与抛物线c:y=x2+2x-3(-3<x<1)相切于点P,则点P的横坐标恰好是方程
x+d与抛物线c:y=x2+2x-3(-3<x<1)相切于点P,则点P的横坐标恰好是方程![]() x+d=x2+2x-3,即2x2+3x-2d-6=0(-3<x<1)的两个相等实数根,解△=9+8(2d+6)=0得d=
x+d=x2+2x-3,即2x2+3x-2d-6=0(-3<x<1)的两个相等实数根,解△=9+8(2d+6)=0得d=![]() ,
,
∴点P的坐标为(![]() ).
).
①当直线l经过点B(1,0)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
②当直线l经过点P(![]() )时,直线l与这个新图象有且只有三个公共点,解得d=
)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
∴综合①、②得:d=![]() 或d=
或d=![]()
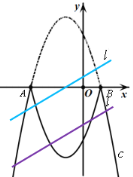
(3)①由平移直线l可得:直线l从经过点A(-3,0)开始向下平移到直线l经过点P(![]() )的过程中,直线l与这个新图象有且只有两个公共点,可得
)的过程中,直线l与这个新图象有且只有两个公共点,可得![]() <d<
<d<![]()
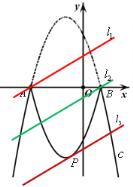
②直线l从经过点P(![]() )继续向下平移的过程中,直线l与这个新图象有且只有两个公共点,可得d<
)继续向下平移的过程中,直线l与这个新图象有且只有两个公共点,可得d<![]() ;
;
∴综合①、②得:![]() <d<
<d<![]() 或d<
或d<![]() ;
;
(4)如图:当直线l经过点B(1,0)时,直线l与这个新图象有且只有三个公共点,解得d=![]() ;
;
当直线l继续向下平移的过程中经过点P(![]() ),直线l与这个新图象有且只有三个公共点,可得d=
),直线l与这个新图象有且只有三个公共点,可得d=![]() ;
;
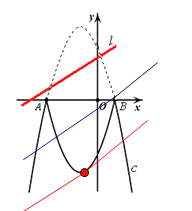
∴要使直线l与这个新图象有四个公共点则d的取值范围是![]() <d<
<d<![]() .
.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案