题目内容
【题目】用适当的方法解方程
(1)![]() (用配方法)
(用配方法)
(2)![]()
(3)![]() (用因式分解法)
(用因式分解法)
(4)![]()
【答案】(1)![]() ,
,![]() ;(2)
;(2)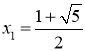 ,
,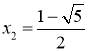 ;(3)
;(3)![]() ,
,![]() ;(4)
;(4)![]() ,
,![]()
【解析】
(1)首先将常数项移到等号的右侧,将等号左右两边同时加上一次项系数一半的平方,即可将等号左边的代数式写成完全平方形式;
(2)先把方程化成一元二次方程的一般式,再找出方程中二次项系数a,一次项系数b及常数项c,计算出b2-4ac为5大于0,然后将a,b及c的值代入求根公式,即可求出原方程的解;
(3)先把方程右边的整式移项并提公因式,再提组间公因式求解即可解答;
(4)先把方程化成一元二次方程的一般式,再利用因式分解法求解即可解答.
解:(1)移项得:![]()
配方得:![]() ,
,
即![]() ,
,
开方得:![]() ,
,
解得:![]() ,
,![]() .
.
(2)![]() (选择适当的方法解)
(选择适当的方法解)
解:![]()
![]()
这里![]() ,
,![]() ,
,![]()
∴![]()
∴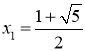 ,
,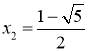
(3)![]()
解:![]()
![]()
![]()
![]() ,
,![]()
∴![]() ,
,![]()
(4)![]()
解:![]()
![]()
![]()
![]() 或
或![]()
∴![]() ,
,![]()

练习册系列答案
相关题目