题目内容
2.加工某种机器零件,要经过三道工序,第一道工序每名工人每小时可完成6个零件,第二道工序每名工人每小时可完成10个零件,第三道工序每名工人每小时可完成15个零件.要使加工生产均衡,三道工序最少共需要( )名工人.| A. | 15 | B. | 10 | C. | 8 | D. | 12 |
分析 先根据题意列出方程6a=10b=15c,由于a,b,c是正整数,得出a是5的倍数,最后由三道工序的工人最少,即可得出a=5即可.
解答 解:设第一道工序安排a名工人,第二道工序安排b名工人,第三道工序安排c名工人,(a,b,c均为正整数)
∵要使加工生产均衡,
则有6a=10b=15c,
∴b=$\frac{3}{5}$a,c=$\frac{2}{5}$a,
∵a,b,c均为正整数,
∴a必是5的倍数,
∵三道工序共需要工人最少,
∴a=5,
∴b=3,c=2,
即第一道工序安排5名工人,第二道工序安排3名工人,第三道工序安排2名工人,
总共5+3+2=10名工人,
故选B.
点评 此题主要考查列不定方程组和不定方程组的整数解的确定,是一道比较简单的题目.

练习册系列答案
相关题目
 的图象经过点B,则k的值是( )
的图象经过点B,则k的值是( )
 D.
D. 
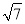 的值是( )
的值是( ) 如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?
如图,计划围一个面积为50m2的长方形场地,一边靠旧墙(墙长为10m),另外三边用篱笆围成,并且它的长与宽之比为5:2.讨论方案时,小英说:“我们不可能围成满足要求的长方形场地.”小军说:“面积和长宽比例是确定的,肯定可以围得出来.”请你判断谁的说法正确,为什么?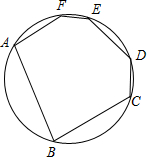 如图,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=140°.
如图,在⊙O的内接六边形ABCDEF中,∠A+∠C=220°,则∠E=140°. 如图,已知直线l,点A是直线l外一点,用尺规作l的垂线,使它经过点A(保留作图痕迹,不写作法)
如图,已知直线l,点A是直线l外一点,用尺规作l的垂线,使它经过点A(保留作图痕迹,不写作法)