题目内容
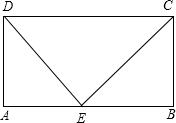如图，已知矩形ABCD中，AD=a，DC=b，在AB上找一点E，使点E与点C、D的连线将矩形分成的三个三角形相似．设AE=x，请问这样的点E是否存在？若存在，这样的点E有几个？若不存在，请说明理由．
分析：根据相似三角形的性质建立a、b、x的二次方程，由根的判别式分析讨论点E的情况．
解答：
解：假设这样的点E存在，由三个三角形相似知：
=
，即
=
，
∴x2-bx+a2=0，
由于△=b2-4a2，
即（1）当b=2a时，△=0，这样的点E只有一个；
（2）当b＞2a时，△＞0，这样的点E只有两个；
（3）当b＜2a时，△＜0，这样的点E不存在．
解：假设这样的点E存在，由三个三角形相似知：| AD |
| AE |
| BE |
| BC |
| a |
| x |
| b-x |
| a |
∴x2-bx+a2=0，
由于△=b2-4a2，
即（1）当b=2a时，△=0，这样的点E只有一个；
（2）当b＞2a时，△＞0，这样的点E只有两个；
（3）当b＜2a时，△＜0，这样的点E不存在．
点评：本题主要利用了相似三角形的性质和一元二次方程的根与系数的关系求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知矩形DEFG内接于Rt△ABC，D在AB上，E、F在BC上，G在AC上，∠BAC=90°，AB=6cm，AC=8cm，
m/秒的速度移动，如果M、N两点同时出发，移动的时间为x秒（0≤x≤6）．
点A运动．
（2012•宁德质检）如图，已知Rt△ABC，∠B=90°，AB=8，BC=6，把斜边AC平均分成n段，以每段为对角线作边与AB、BC平行的小矩形，则这些小矩形的面积和是（ ）
如图，已知矩形ABCD中AB：BC=3：1，点A、B在x轴上，直线y=mx+n（0＜m＜n＜