Question

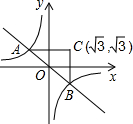（2008•雅安）如图，反比例函数y=-

3

x

与一次函数y=-x的图象交于A、B两点．
（1）求A、B两点的坐标．
（2）若点C（

3

，

3

），求△ABC的面积．

Answer 1

分析：（1）根据反比例函数与一次函数的交点坐标同时满足两个函数的解析式可解方程组

y=- 3 x y=-x

得到A与B的坐标；
（2）根据A、B、C的坐标特点得到AC⊥BC，∠ACB=90°，然后利用三角形面积公式求解．

解答：解：（1）根据题意得

y=- 3 x y=-x

，
解方程组得

x= 3 y=- 3

或

x=- 3 y= 3

，
故A点坐标为（-

3

，

3

），B点坐标为（

3

，-

3

）；

（2）∵点C（

3

，

3

），
∴AC⊥BC，
∴∠ACB=90°，
∴△ABC的面积=

1

2

AC•BC=

1

2

×2

3

×2

3

=6．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的交点坐标同时满足两个函数的解析式．