题目内容
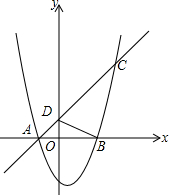 如图,一次函数y=x+m的图象经过点A(-2,0),交y轴于点D,对称轴为x=1的抛物线与x轴相交于点A、B,并与直线AD相交于点C,连接BD、BC,有∠OBD=∠BCD.
如图,一次函数y=x+m的图象经过点A(-2,0),交y轴于点D,对称轴为x=1的抛物线与x轴相交于点A、B,并与直线AD相交于点C,连接BD、BC,有∠OBD=∠BCD.(1)求点B、C、D的坐标;
(2)求抛物线的函数解析式;
(3)抛物线上是否存在点P,使∠ACP为直角?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由A的坐标和对称轴即可求得B的坐标,把A的坐标代入一次函数解析式求得m的值即可求得D的坐标,然后通过△ABD∽△ACB和平行线分线段成比例定理即可求得C的坐标;
(2)把A、B、C的坐标代入解析式,根据待定系数法即可求得抛物线的解析式;
(3)过C点作CF⊥AC,交x轴于F,根据等腰直角三角形求得F的坐标,然后根据待定系数法求得直线CF的解析式,然后和抛物线的解析式联立方程,即可求得P的坐标.
(2)把A、B、C的坐标代入解析式,根据待定系数法即可求得抛物线的解析式;
(3)过C点作CF⊥AC,交x轴于F,根据等腰直角三角形求得F的坐标,然后根据待定系数法求得直线CF的解析式,然后和抛物线的解析式联立方程,即可求得P的坐标.
解答: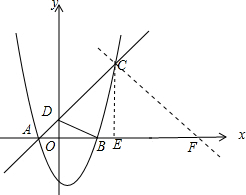 解:(1)∵抛物线与x轴相交于点A、B,且对称轴为x=1,A(-2,0),
解:(1)∵抛物线与x轴相交于点A、B,且对称轴为x=1,A(-2,0),
∴B的坐标为(4,0),
∴AB=2+4=6,
∵一次函数y=x+m的图象经过点A(-2,0),
∴-2+m=0,解得m=2,
∴D的坐标为(0,2),
∴AD=
=
=2
,
在△ABD和△ACB中,∠ABD=∠BCA,∠DAB=∠BAC,
∴△ABD∽△ACB,
∴
=
,
∴AC=
=9
,
作CE∥y轴,
∴
=
=
=
=
,
∴AE=
=9,CE=
=9,
∴OE=AE-OA=7,
∴C的坐标为(7,9);
(2)∵二次函数y=ax2+bx+c的图象过A(-2,0),B(4,0),C(7,9),
∴
,解得
,
∴抛物线的函数解析式为y=
x2-
x-
.
(3)存在;
过C点作CF⊥AC,交x轴于F,
∴OA=OD=2,
∴∠CAF=45°,
∴△CAF是等腰直角三角形,
∴AE=EF=9,
∴F的坐标(16,0),
设直线CF的函数解析式为y=kx+b,
∴
,解得
,
∴直线CF的函数解析式为y=-x+16,
解
,得
或
,
∴P的坐标为(-8,24).
所以抛物线上存在点P,使∠ACP为直角,此时P的坐标为(-8,24).
 解:(1)∵抛物线与x轴相交于点A、B,且对称轴为x=1,A(-2,0),
解:(1)∵抛物线与x轴相交于点A、B,且对称轴为x=1,A(-2,0),∴B的坐标为(4,0),
∴AB=2+4=6,
∵一次函数y=x+m的图象经过点A(-2,0),
∴-2+m=0,解得m=2,
∴D的坐标为(0,2),
∴AD=
| OA2+OD2 |
| 22+22 |
| 2 |
在△ABD和△ACB中,∠ABD=∠BCA,∠DAB=∠BAC,
∴△ABD∽△ACB,
∴
| AC |
| AB |
| AB |
| AD |
∴AC=
| 6×6 | ||
2
|
| 2 |
作CE∥y轴,
∴
| AE |
| OA |
| CE |
| OD |
| AC |
| AD |
9
| ||
2
|
| 9 |
| 2 |
∴AE=
| 2×9 |
| 2 |
| 2×9 |
| 2 |
∴OE=AE-OA=7,
∴C的坐标为(7,9);
(2)∵二次函数y=ax2+bx+c的图象过A(-2,0),B(4,0),C(7,9),
∴
|
|
∴抛物线的函数解析式为y=
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 3 |
(3)存在;
过C点作CF⊥AC,交x轴于F,
∴OA=OD=2,
∴∠CAF=45°,
∴△CAF是等腰直角三角形,
∴AE=EF=9,
∴F的坐标(16,0),
设直线CF的函数解析式为y=kx+b,
∴
|
|
∴直线CF的函数解析式为y=-x+16,
解
|
|
|
∴P的坐标为(-8,24).
所以抛物线上存在点P,使∠ACP为直角,此时P的坐标为(-8,24).
点评:本题考查了二次函数的综合题,解题的关键是应用待定系数法求解析式,三角形相似的判定和性质,等腰直角三角形的判定和性质.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
一个立体图形三视图如图所示,那么这个立体图形的名称是( )

| A、三棱柱 | B、四棱柱 |
| C、三棱锥 | D、四棱锥 |
下列运算中,正确的是( )
| A、a2+a2=a4 |
| B、(a-b)2=a2-b2 |
| C、-a(1-a)=a2-a |
| D、a3•a-4=a-12 |
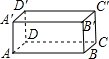 如图是一个放置雕塑的长方形底座,AB=12米,BC=2米,BB′=3米.一只蚂蚁从A点出发,以2厘米/秒的速度沿长方形表面爬到C′至少需要
如图是一个放置雕塑的长方形底座,AB=12米,BC=2米,BB′=3米.一只蚂蚁从A点出发,以2厘米/秒的速度沿长方形表面爬到C′至少需要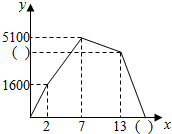 甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.
甲骑自行车,乙步行均从A地出发,以各自的速度匀速向B地行驶,其中甲先出发到达B地,停留6分钟后,按原路原速返回到A地,乙则一直步行到B地,如图是甲乙两人之间的距离y米与甲用时x之间的部分函数图象.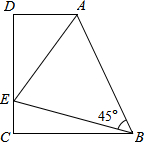 如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度.
如图,在梯形ABCD中,AD∥BC(BC>AD),∠D=90°,BC=CD=12,∠ABE=45°,若AE=10.求CE的长度. 如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为
如图,二次函数y=ax2+mc(a≠0)的图象经过正方形ABOC的三个顶点,且ac=-2,则m的值为