题目内容
某直角三角形的周长为30，且一条直角边长为5，求另一条直角边的长．
考点：勾股定理
专题：
分析：设另一条直角边的长为x，根据三角形的周长的定义表示出斜边，再利用勾股定理列出方程求解即可．
解答：解：设另一条直角边的长为x，
则斜边为：30-5-x=25-x，
由勾股定理得，x2+52=（25-x）2，
解得x=12．
答：另一条直角边的长12．
则斜边为：30-5-x=25-x，
由勾股定理得，x2+52=（25-x）2，
解得x=12．
答：另一条直角边的长12．
点评：本题考查了勾股定理，读懂题目信息，利用勾股定理列出方程是解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
若二次函数的图象的顶点坐标为（2，-1），且抛物线过（0，3），则二次函数的解析式是（ ）
| A、y=-（x-2）2-1 | ||
B、y=-
| ||
| C、y=（x-2）2-1 | ||
D、y=
|
如图是抛物线y=ax2+bx+c的图象，则由图象可知，不等式ax2+bx+c＜0的解集是若a表示有理数，则-a是（ ）
| A、正数 | B、负数 |
| C、a的相反数 | D、a的倒数 |
如图所示，在平行四边形ABCD中，对角线AC、BD交于O点，过O点作直线交AD于E，交BC于F，图中能够全等的三角形共有（ ）| A、2对 | B、4对 | C、6对 | D、8对 |
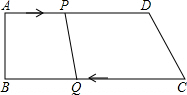在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=25cm，BC=26cm；点P从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动．规定其中一个动点到达端点时另一个动点也停止运动，从运动开始．使PQ=CD，需经过多少时间？
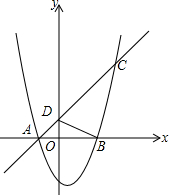如图，一次函数y=x+m的图象经过点A（-2，0），交y轴于点D，对称轴为x=1的抛物线与x轴相交于点A、B，并与直线AD相交于点C，连接BD、BC，有∠OBD=∠BCD．