题目内容
10.若x,y分别表示5-$\sqrt{7}$的整数部分和小数部分,则x-y=$\sqrt{7}$-1.分析 先用夹逼法估算$\sqrt{7}$的值,再根据不等式的性质得到x,y的值,代入x-y计算即可.
解答 解:∵$\sqrt{4}$<$\sqrt{7}$<$\sqrt{9}$,
∴2<$\sqrt{7}$<3,
∴-3<-$\sqrt{7}$<-2,
∴2<5-$\sqrt{7}$<3,
∴x=2,y=5-$\sqrt{7}$-2=3-$\sqrt{7}$,
∴x-y=2-(3-$\sqrt{7}$)=$\sqrt{7}$-1.
故答案为:$\sqrt{7}$-1.
点评 此题主要考查估算无理数的大小,应用夹逼法估算$\sqrt{7}$的值是解题的关键.

练习册系列答案
相关题目
2.一次函数y=2x+b的图象与y轴的交点坐标为(0,-2),则b=( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
18.如图,每一幅图中均含有若干个正方形,第1幅图中有1个正方形;第2幅图中有5个正方形;按这样的规律下去,第6幅图中有( )个正方形.


| A. | 90 | B. | 91 | C. | 140 | D. | 141 |
5.(-$\frac{5}{13}$)2015×(-2$\frac{3}{5}$)2016的值是( )
| A. | -1 | B. | 1 | C. | -$\frac{13}{5}$ | D. | $\frac{5}{13}$ |
 B.
B. 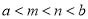
 D.
D. 
 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6.
小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系是h=n+6. 如图,在⊙O中,弦AB、CD相交于点M,连接BC、AD,∠AMD=100°,∠A=30°,则∠B=50°.
如图,在⊙O中,弦AB、CD相交于点M,连接BC、AD,∠AMD=100°,∠A=30°,则∠B=50°.