题目内容
完成下列有关正多边形的计算:
| 正多边形边数 | 内角 | 中心角 | 半径 | 边长 | 边心距 | 周长 | 面积 | ||
| 3 | 60° | 2
| |||||||
| 4 | 1 | ||||||||
| 6 |
|
考点:正多边形和圆
专题:
分析:首先根据题意画出图形,然后根据含30°角的直角三角形的性质、等腰直角三角形的性质以及等边三角形的性质求解即可求得答案.
解答: 解:如图(1)中心角∠BOC=
解:如图(1)中心角∠BOC=
=120°,
∵∠OBD=
∠ABC=30°,CB=2
,
∴OD=1,
∴BD=
,
OB=2,
即半径为2,边心距为1,
∴周长为:6
,
∴面积为:
BC•OD×3=3
;
如图(2),内角∠A=90°,中心角∠BOC=90°,
∴△BOC、△OBE是等腰直角三角形,
∵边心距OE=
,
∴BC=2OE=2,OB=
OE=
,
∴半径为:
,边长为2,
∴周长为8,面积为4;
如图(3),内角120°,中心角∠AOB=
=60°,
∴△OAB是等边三角形,
∵边心距OE=
,
∴AM=
=1,
∴AB=OA=2AM=2,
∴半径为:2,边长为2,
∴周长为12,面积为:6S△AOB=6×
AB•OM=6
.
故答案为:
 解:如图(1)中心角∠BOC=
解:如图(1)中心角∠BOC=| 360° |
| 3 |
∵∠OBD=
| 1 |
| 2 |
| 3 |
∴OD=1,
∴BD=
| 3 |
OB=2,
即半径为2,边心距为1,
∴周长为:6
| 3 |
∴面积为:
| 1 |
| 2 |
| 3 |
如图(2),内角∠A=90°,中心角∠BOC=90°,
∴△BOC、△OBE是等腰直角三角形,
∵边心距OE=
| 3 |
∴BC=2OE=2,OB=
| 2 |
| 2 |
∴半径为:
| 2 |
∴周长为8,面积为4;
如图(3),内角120°,中心角∠AOB=
| 360° |
| 6 |
∴△OAB是等边三角形,
∵边心距OE=
| 3 |
∴AM=
| OM |
| tan60° |
∴AB=OA=2AM=2,
∴半径为:2,边长为2,
∴周长为12,面积为:6S△AOB=6×
| 1 |
| 2 |
| 3 |
故答案为:
| 正多边形边数 | 内角 | 中心角 | 半径 | 边长 | 边心距 | 周长 | 面积 | ||||||
| 3 | 60° | 120° | 2 | 2
| 1 | 6
| 3
| ||||||
| 4 | 90° | 90° |
| 2 | 1 | 8 | 4 | ||||||
| 6 | 120° | 60° | 2 | 2 |
| 12 | 6
|
点评:本题考查了正多边形与圆的知识.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
如图所示图形中,不是正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
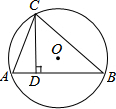 如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积.
如图,△ABC内接于⊙O,CD是△ABC的高,CD=6,AD=3,BD=8,求⊙O的面积. 如图,直角三角形的两直角边AC=6cm,BC=8cm,沿AD折叠使AC落在AB上.点C与E重合,折痕为AD,试求CD的长.
如图,直角三角形的两直角边AC=6cm,BC=8cm,沿AD折叠使AC落在AB上.点C与E重合,折痕为AD,试求CD的长. 在正方形ABCD中,对角线AC、BD相交于O,AE平分∠BAC交BD于E,若正方形ABCD的周长为16,则DE=
在正方形ABCD中,对角线AC、BD相交于O,AE平分∠BAC交BD于E,若正方形ABCD的周长为16,则DE=