题目内容
若关于 的方程
的方程 的两根互为倒数,则
的两根互为倒数,则 .
.
-1.
【解析】
试题分析:设方程的两根分别为m与n,由m与n互为倒数得到mn=1,再由方程有解,得到根的判别式大于等于0,列出关于a的不等式,求出不等式的解集得到a的范围,然后利用根与系数的关系表示出两根之积,可得出关于a的方程,求出方程的解得到a的值即可.
试题解析:设已知方程的两根分别为m,n,
由题意得:m与n互为倒数,即mn=1,
由方程有解,得到△=b2-4ac=(a-1)2-4a2≥0,
解得:-1≤a≤ ,
,
又mn=a2,
∴a2=1,
解得:a=1(舍去)或a=-1,
则a=-1.
考点:根与系数的关系.

练习册系列答案
相关题目
 的根的情况是( )
的根的情况是( )
 、
、 是方程
是方程 的两个根,则代数式
的两个根,则代数式 的值为 .
的值为 .
 ) B.(-1,
) B.(-1, ) C.(
) C.( ,0) D.(1,
,0) D.(1, )
)
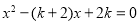 .
. 取何值时,这个方程一定有实数根;
取何值时,这个方程一定有实数根; ,另两边长
,另两边长 、
、 恰好是这个方程的两个根 ,求△ABC的周长.
恰好是这个方程的两个根 ,求△ABC的周长.