题目内容
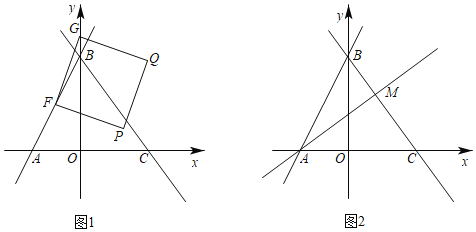
【题目】如图，在平面直角坐标系中，直线y＝2x+4与x轴交于点A，与y轴交于点B，过点B的直线交x轴于C，且△ABC面积为10．
（1）求点C的坐标及直线BC的解析式；
（2）如图1，设点F为线段AB中点，点G为y轴上一动点，连接FG，以FG为边向FG右侧作正方形FGQP，在G点的运动过程中，当顶点Q落在直线BC上时，求点G的坐标；
（3）如图2，若M为线段BC上一点，且满足S△AMB＝S△AOB，点E为直线AM上一动点，在x轴上是否存在点D，使以点D，E，B，C为顶点的四边形为平行四边形？若存在，请直接写出点D的坐标；若不存在，请说明理由．
【答案】（1）C（3，0），直线BC的解析式为y＝﹣
x+4；（2）满足条件的点G坐标为（0，
）或（0，﹣1）；（3）存在，满足条件的点D的坐标为（
，0）或（﹣
，0）或（﹣
，0）
【解析】
（1）利用三角形的面积公式求出点
坐标，再利用待定系数法即可解决问题．
（2）分两种情形：①当
时，如图
中，点
落在
上时，过
作直线平行于
轴，过点
，作该直线的垂线，垂足分别为
，
．求出
．②当
时，如图
中，同法可得
，利用待定系数法即可解决问题．
（3）利用三角形的面积公式求出点的坐标，求出直线
的解析式，作
交直线于
，此时
，
，当
时，可得四边形
，四边形
是平行四边形，可得
，
，
，，再根据对称性可得
解决问题．
解：（1）
直线
与轴交于点
，与
轴交于点
，
，
，
，
，
，
，
，
，
设直线的解析式为
，则有
，
．
直线的解析式为
．
（2）
，
，，
，设
，
①当时，如图中，点落在上时，过作直线平行于轴，过点，作该直线的垂线，垂足分别为，．
四边形
是正方形，易证
，
，
，
，
点在直线上，
，
，
．
②当时，如图中，同法可得，
点在直线上，
，
，
．
综上所述，满足条件的点坐标为
或
．
（3）如图3中，设
，
，
，
，
，
，
，
直线的解析式为
，
作交直线于，此时，，
当时，可得四边形，四边形是平行四边形，可得，，，，
根据对称性可得点
关于点的对称点
，也符合条件，
综上所述，满足条件的点的坐标为
，或
，或
，．
