题目内容
【题目】某广告公司为了招聘一名创意策划，准备从专业技能和创新能力两方面进行考核，成绩高者录取．甲、乙、丙三名应聘者的考核成绩以百分制统计如下：
（1）如果公司认为专业技能和创新能力同等重要，则应聘人 将被录取．
（2）如果公司认为职员的创新能力比专业技能重要，因此分别赋予它们6和4的权．计算他们赋权后各自的平均成绩，并说明谁将被录取．
【答案】（1）甲 （2）乙将被录取
【解析】
（1）根据题意分别求出甲、乙、丙三名应聘者的平均成绩进行比较即可；
（2）由题意利用加权平均数计算他们赋权后各自的平均成绩，从而进行说明.
解: （1）根据公司认为专业技能和创新能力同等重要，即是求甲、乙、丙三名应聘者的平均成绩：
甲：
；
乙：
；
丙：
；
所以应聘人甲将被录取．
（2）甲: 
；
乙：
；
丙：
；
所以乙将被录取.
练习册系列答案
文敬图书课时先锋系列答案
相关题目
【题目】为了解某区八年级学生的睡眠情况，随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人，利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表（单位：小时）
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
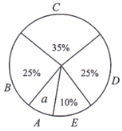
根据图表提供的信息，回答下列问题：
（1）试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数；
（2）如果睡眠时间x（时）满足：
，称睡眠时间合格.已知该区八年级学生有3250人，试估计该区八年级学生睡眠时间合格的共有多少人？
（3）如果将各组别学生睡眠情况分组的最小值（如C组别中，取
），B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
