题目内容
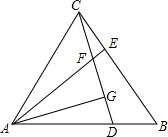 如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G,下列结论:①AE=CD;②∠AFC=120°;③△ADF是等边三角形,其中正确的结论是
如图,等边三角形ABC中,D、E分别在AB、BC边上,且AD=BE,AE与CD交于点F,AG⊥CD于点G,下列结论:①AE=CD;②∠AFC=120°;③△ADF是等边三角形,其中正确的结论是考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:①由等边三角形的性质就可以得出△ADC≌△BEA,就有∠ACD=∠BAE,CD=AE;
②由三角形的外角与内角的关系可以得出∠AFC=∠ADC+∠DAE=∠ADC+∠DCA,根据三角形的内角和就可以求出结论;
③由∠AFC=120°就可以得出∠AFD=60°,∠ADC=∠B+∠BCD>60°,故△ADF不是等边三角形.
②由三角形的外角与内角的关系可以得出∠AFC=∠ADC+∠DAE=∠ADC+∠DCA,根据三角形的内角和就可以求出结论;
③由∠AFC=120°就可以得出∠AFD=60°,∠ADC=∠B+∠BCD>60°,故△ADF不是等边三角形.
解答:解:①∵△ABC是等边三角形,
∴AB=BC=AC,∠CAB=∠ABC=∠ACB=60°.
在△BEA和△ADC中
,
∴△BEA≌△ADC(SAS),
∴AE=CD
∠BAE=∠ACD;
②∵∠AFC=∠ADC+∠DAE,
∴∠AFC=∠ADC+∠DCA.
∵∠ADC+∠DCA+∠BAC=180°,
∴∠ADC+∠DCA=120°,
∴∠AFC=120°;
③∵∠AFC+∠AFD=180°,
∴∠AFD=60°.
∵∠ADC=∠BCD+∠B,
∴∠ADC=∠BCD+60°≠60°,
∴∠AFD≠∠ADC≠∠DAF≠60°,
∴△ADF不是等边三角形.
故正确的有①②.
故答案为:①②.
∴AB=BC=AC,∠CAB=∠ABC=∠ACB=60°.
在△BEA和△ADC中
|
∴△BEA≌△ADC(SAS),
∴AE=CD
∠BAE=∠ACD;
②∵∠AFC=∠ADC+∠DAE,
∴∠AFC=∠ADC+∠DCA.
∵∠ADC+∠DCA+∠BAC=180°,
∴∠ADC+∠DCA=120°,
∴∠AFC=120°;
③∵∠AFC+∠AFD=180°,
∴∠AFD=60°.
∵∠ADC=∠BCD+∠B,
∴∠ADC=∠BCD+60°≠60°,
∴∠AFD≠∠ADC≠∠DAF≠60°,
∴△ADF不是等边三角形.
故正确的有①②.
故答案为:①②.
点评:本题考查了等边三角形的性质的运用,全等三角形的判定及性质的运用,三角形的外角与内角的关系的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥BD于F,PE⊥AC于E,则PE+PF的值为( )
如图,在矩形ABCD中,AB=3,AD=4,P是AD上一动点,PF⊥BD于F,PE⊥AC于E,则PE+PF的值为( )A、
| ||
B、
| ||
C、
| ||
| D、5 |
不等式1-2x<5-
x的负整数解有( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
若a,b为实数,下列选项中真命题是( )
| A、若a>b,则a2>b2 | ||
B、若a=
| ||
| C、若|a|=|b|,则a=b | ||
| D、若a2>b2,则a>b |
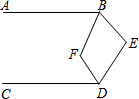 如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E=110°,则∠BFD的度数为 如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为8cm,则MN的长为
如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为8cm,则MN的长为 如图,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,则阴影部分面积是
如图,两个完全相同的直角梯形重叠在一起,将其中一个直角梯形沿AD的方向平移,则阴影部分面积是