Question

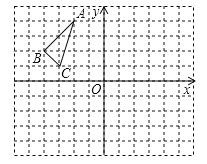
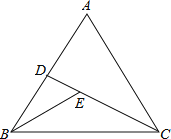
【题目】如图，在等边△ABC中，D为AB上一点，连接CD，在CD上取一点E，连接BE，且∠BED＝60°，若CE＝5，△ACD的面积为，则线段DB的长为_____．

Answer 1

【答案】

【解析】

延长BE交AC边于点F，易证△ACD≌△CBF，得BF=CD，利用三角形的面积求出BF的长度，继而求出DE的长度；然后证明△BED∽△CBD，即可求得BD的长度．

如图，延长BE交AC边于点F，

因为∠FCD+∠DCB=60°，∠DEB=∠EBC+∠ECB=60°，

∴∠ACD=∠FBC，

在△ACD和△CBF中，

∴△ACD≌△CBF，

∴BF=CD，

，

∴，则，

∵，

∴∠DBE=∠DCB，∠DEB=∠DBC=60，

△BED∽△CBD，

∴，

，

∴BD=．