题目内容
17.先化简,再求值:$\frac{{x}^{2}-18x+81}{{x}^{3}-9{x}^{2}}$÷(1-$\frac{81}{{x}^{2}}$),其中x=$\sqrt{3}$-9.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{(x-9)^{2}}{{x}^{2}(x-9)}$÷$\frac{{x}^{2}-81}{{x}^{2}}$=$\frac{(x-9)^{2}}{{x}^{2}(x-9)}$•$\frac{{x}^{2}}{(x+9)(x-9)}$=$\frac{1}{x+9}$,
当x=$\sqrt{3}$-9时,原式=$\frac{\sqrt{3}}{3}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
7.若x=5是关于x的方程2x+3m-1=0的解,则m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -3 |
5.下列运算正确的是( )
| A. | (a2)3=a5 | B. | a+2a=3a2 | C. | a6•a3=a9 | D. | (a-b)2=a2-b2 |

 如图,在平面直角坐标系中,四边形OABC是平行四边形,AB=2,OA=$\sqrt{2}$,∠AOC=45°,则B点的坐标是(-3,1).
如图,在平面直角坐标系中,四边形OABC是平行四边形,AB=2,OA=$\sqrt{2}$,∠AOC=45°,则B点的坐标是(-3,1).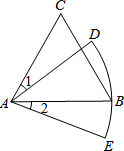 如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).
如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).