题目内容
平面直角坐标系xOy中,抛物线y=ax2-4ax+4a+c与x轴交于点A、点B,与y轴的正半轴交于点C,点 A的坐标为(1,0),OB=OC,抛物线的顶点为D.
(1)求此抛物线的解析式;
(2)作出△ABC的外接圆;
(3)若此抛物线的对称轴上的点P满足∠APB<∠ACB,求出点P的纵坐标的取值范围;
(4)Q为线段BD上一点,点A关于∠AQB的平分线的对称点为A′,若QA-QB=
,请直接写出点Q的坐标.
(1)求此抛物线的解析式;
(2)作出△ABC的外接圆;
(3)若此抛物线的对称轴上的点P满足∠APB<∠ACB,求出点P的纵坐标的取值范围;
(4)Q为线段BD上一点,点A关于∠AQB的平分线的对称点为A′,若QA-QB=
| 2 |
考点:二次函数综合题
专题:
分析:(1)首先将已知的抛物线解析式进行配方,得出对称轴方程后结合A点坐标可确定B点的坐标,由OB=OC的条件能得到C点坐标,利用待定系数法即可确定函数的解析式.
(2)作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F就是△ABC的外接圆;
(3)由点F的坐标为(2,2),可得当∠APB<∠ACB,对称轴上的点P纵坐标>2或P纵坐标<-2时,∠APB<∠ACB,
(4)A、A′关于角平分线对称,那么QA、QA′也关于该角平分线对称,即QA=QA′,那么QA-QB的长其实就是AB的长,可由这个条件入手解答;易知点D、B的坐标,能求出∠ABD的度数(或相关三角函数值),过A′作A′N⊥x轴,在构建的Rt△A′BN中,∠A′BN的度数已求出,可得到BN、A′N的长,即可求出A′的坐标和直线A′B的解析式,然后设出点Q坐标,表示出AQ、A′Q的长,以这两条线段相等作为等量条件求出点Q的坐标.
(2)作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F就是△ABC的外接圆;
(3)由点F的坐标为(2,2),可得当∠APB<∠ACB,对称轴上的点P纵坐标>2或P纵坐标<-2时,∠APB<∠ACB,
(4)A、A′关于角平分线对称,那么QA、QA′也关于该角平分线对称,即QA=QA′,那么QA-QB的长其实就是AB的长,可由这个条件入手解答;易知点D、B的坐标,能求出∠ABD的度数(或相关三角函数值),过A′作A′N⊥x轴,在构建的Rt△A′BN中,∠A′BN的度数已求出,可得到BN、A′N的长,即可求出A′的坐标和直线A′B的解析式,然后设出点Q坐标,表示出AQ、A′Q的长,以这两条线段相等作为等量条件求出点Q的坐标.
解答:解:(1)如图1,

∵y=ax2-4ax+4a+c=a(x-2)2+c,
∴抛物线的对称轴为直线x=2.
∵抛物线y=ax2-4ax+4a+c与x轴交于点A、点B,点A的坐标为(1,0),
∴点B的坐标为(3,0),OB=3.
可得该抛物线的解析式为y=a(x-1)(x-3).
∵OB=OC,抛物线与y轴的正半轴交于点C,
∴OC=3,点C的坐标为(0,3).
将点C(0,3)代入该解析式y=a(x-1)(x-3).
解得a=1.
∴此抛物线的解析式为y=x2-4x+3.
(2)如图2,作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F就是△ABC的外接圆;

(3)由图2可得,点F的坐标为(2,2)
∴当∠APB<∠ACB,对称轴上的点P纵坐标>2或P纵坐标<-2时,∠APB<∠ACB,
(4)∵点B、D的坐标分别为B(3,0)、D(2,-1),
可得直线BD的解析式为y=x-3,直线BD与x轴所夹的锐角为45°.
∵点A关于∠AQB的平分线的对称点为A',如图3,

若设AA'与∠AQB的平分线的交点为M,
则有 QA=QA',AM=A'M,AA'⊥QM,Q,B,A'三点在一条直线上.
∵QA-QB=
,
∴BA'=QA'-QB=QA-QB=
,
作A'N⊥x轴于点N.
∵点Q在线段BD上,Q,B,A'三点在一条直线上,
∴A'N=BA'•sin45°=1,BN=BA'•cos45°=1.
∴点A'的坐标为(4,1).
∵点Q在线段BD上,
∴设点Q的坐标为Q(x,x-3),其中2<x<3.
∵QA=QA',
∴由两点间的距离公式得 (x-1)2+(x-3)2=(x-4)2+(x-3-1)2,
解得x=
,经检验,x=
,在2<x<3的范围内.
∴点Q的坐标为Q(
,-
).

∵y=ax2-4ax+4a+c=a(x-2)2+c,
∴抛物线的对称轴为直线x=2.
∵抛物线y=ax2-4ax+4a+c与x轴交于点A、点B,点A的坐标为(1,0),
∴点B的坐标为(3,0),OB=3.
可得该抛物线的解析式为y=a(x-1)(x-3).
∵OB=OC,抛物线与y轴的正半轴交于点C,
∴OC=3,点C的坐标为(0,3).
将点C(0,3)代入该解析式y=a(x-1)(x-3).
解得a=1.
∴此抛物线的解析式为y=x2-4x+3.
(2)如图2,作BC的垂线交对称轴于点F,以点F为圆心,以FB为半径作⊙F就是△ABC的外接圆;

(3)由图2可得,点F的坐标为(2,2)
∴当∠APB<∠ACB,对称轴上的点P纵坐标>2或P纵坐标<-2时,∠APB<∠ACB,
(4)∵点B、D的坐标分别为B(3,0)、D(2,-1),
可得直线BD的解析式为y=x-3,直线BD与x轴所夹的锐角为45°.
∵点A关于∠AQB的平分线的对称点为A',如图3,

若设AA'与∠AQB的平分线的交点为M,
则有 QA=QA',AM=A'M,AA'⊥QM,Q,B,A'三点在一条直线上.
∵QA-QB=
| 2 |
∴BA'=QA'-QB=QA-QB=
| 2 |
作A'N⊥x轴于点N.
∵点Q在线段BD上,Q,B,A'三点在一条直线上,
∴A'N=BA'•sin45°=1,BN=BA'•cos45°=1.
∴点A'的坐标为(4,1).
∵点Q在线段BD上,
∴设点Q的坐标为Q(x,x-3),其中2<x<3.
∵QA=QA',
∴由两点间的距离公式得 (x-1)2+(x-3)2=(x-4)2+(x-3-1)2,
解得x=
| 11 |
| 4 |
| 11 |
| 4 |
∴点Q的坐标为Q(
| 11 |
| 4 |
| 1 |
| 4 |
点评:本题主要考查了二次函数题综合题,融合了圆、解直角三角形、轴对称图形等重点知识,使得难度增加不少,解题的关键,应注意并总结转化思想在解题中的妙用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在直角坐标系中y=-3x+2与x轴的交点坐标是( )
A、(
| ||
B、(-
| ||
C、(0,-
| ||
D、(0,
|
某环境检测中心关于2013年1月份第二周的空气质量报告中某项污染指数的数据如表所示,这组数据的众数是( )
| 检测时间 | 周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 |
| 污染指数 | 21 | 22 | 21 | 24 | 20 | 22 | 21 |
| A、20 | B、21 | C、22 | D、24 |
在实数-
,
,
,-0.518,
,0.101001…中,无理数的个数有( )
| 21 |
| 7 |
| 8 |
| 3 | -8 |
| π |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
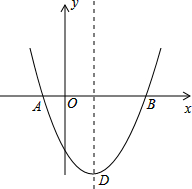 如图,抛物线y=ax2+bx-5交x轴于A(-1,0),B(5,0),顶点为D,交y轴于点C.
如图,抛物线y=ax2+bx-5交x轴于A(-1,0),B(5,0),顶点为D,交y轴于点C.