ЬтФПФкШн
ЁОЬтФПЁПзджїбЇЯАЃЌЧыдФЖСЯТСаНтЬтЙ§ГЬЃЎ
НтвЛдЊЖўДЮВЛЕШЪНЃКx2Љ5xЃО0ЃЎ
НтЃКЩшx2Љ5x=0ЃЌНтЕУЃКx1=0ЃЌx2=5ЃЌдђХзЮяЯпy=x2Љ5xгыxжсЕФНЛЕузјБъЮЊЃЈ0ЃЌ0ЃЉКЭЃЈ5ЃЌ0ЃЉЃЎЛГіЖўДЮКЏЪ§y=x2Љ5xЕФДѓжТЭМЯѓЃЈШчЭМЫљЪОЃЉЃЌгЩЭМЯѓПЩжЊЃКЕБxЃМ0ЃЌЛђxЃО5ЪБКЏЪ§ЭМЯѓЮЛгкxжсЩЯЗНЃЌДЫЪБyЃО0ЃЌМДx2Љ5xЃО0ЃЌЫљвдЃЌвЛдЊЖўДЮВЛЕШЪНx2Љ5xЃО0ЕФНтМЏЮЊЃКxЃМ0ЃЌЛђxЃО5ЃЎ
ЭЈЙ§ЖдЩЯЪіНтЬтЙ§ГЬЕФбЇЯАЃЌАДЦфНтЬтЕФЫМТЗКЭЗНЗЈНтД№ЯТСаЮЪЬтЃК
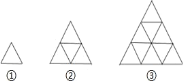
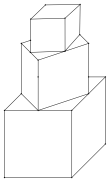
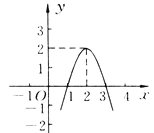
ЃЈ1ЃЉЩЯЪіНтЬтЙ§ГЬжаЃЌЩјЭИСЫЯТСаЪ§бЇЫМЯыжаЕФЁЁ ЁЁКЭЁЁ ЁЁЃЎЃЈжЛЬюађКХЃЉ
ЂйзЊЛЏЫМЯы ЂкЗжРрЬжТлЫМЯы ЂлЪ§аЮНсКЯЫМЯы
ЃЈ2ЃЉвЛдЊЖўДЮВЛЕШЪНx2Љ5xЃМ0ЕФНтМЏЮЊЁЁ ЃЎ
ЃЈ3ЃЉгУРрЫЦЕФЗНЗЈНтвЛдЊЖўДЮВЛЕШЪНЃКx2Љ2xЉ3ЃО0ЃЎ
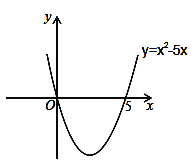
ЁОД№АИЁПЃЈ1ЃЉЂйЃЌЂлЃЈ2ЃЉ0ЃМxЃМ5ЃЈ3ЃЉxЃМЉ1ЃЌЛђxЃО3ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉНтЬтЙ§ГЬжаЃЌЩјЭИСЫзЊЛЏЫМЯыКЭЪ§аЮНсКЯЫМЯыЃЛ
ЃЈ2ЃЉЙлВьЭМЯѓМДПЩаДГівЛдЊЖўДЮВЛЕШЪНЃКx2Љ5xЃМ0ЕФНтМЏЃЛ
ЃЈ3ЃЉЯШЩшКЏЪ§НтЮіЪНЃЌИљОнaЕФжЕШЗЖЈХзЮяЯпЕФПЊПкЯђЩЯЃЌдйевГіХзЮяЯпгыxжсЯрНЛЕФСНЕуЃЌОЭПЩвдЛГіХзЮяЯпЃЌИљОнyЃО0ШЗЖЈвЛдЊЖўДЮВЛЕШЪНx2Љ2xЉ3ЃО0ЕФНтМЏЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЩЯЪіНтЬтЙ§ГЬжаЃЌЩјЭИСЫЯТСаЪ§бЇЫМЯыжаЕФЂйКЭЂлЃЛ
ЙЪД№АИЮЊЃКЂйЃЌЂлЃЛ
ЃЈ2ЃЉгЩЭМЯѓПЩжЊЃКЕБ0ЃМxЃМ5ЪБКЏЪ§ЭМЯѓЮЛгкxжсЯТЗНЃЌДЫЪБyЃМ0ЃЌМДx2Љ5xЃМ0ЃЌЁрвЛдЊЖўДЮВЛЕШЪНx2Љ5xЃМ0ЕФНтМЏЮЊЃК0ЃМxЃМ5ЁЃЙЪД№АИЮЊЃК0ЃМxЃМ5ЃЎ
ЃЈ3ЃЉЩшx2Љ2xЉ3=0ЃЌНтЕУЃКx1=3ЃЌx2=Љ1ЃЌЁрХзЮяЯпy=x2Љ2xЉ3гыxжсЕФНЛЕузјБъЮЊЃЈ3ЃЌ0ЃЉКЭЃЈЉ1ЃЌ0ЃЉЃЎ
ЛГіЖўДЮКЏЪ§y=x2Љ2xЉ3ЕФДѓжТЭМЯѓЃЈШчЭМЫљЪОЃЉЁЃ
гЩЭМЯѓПЩжЊЃКЕБxЃМЉ1ЛђxЃО3ЪБКЏЪ§ЭМЯѓЮЛгкxжсЩЯЗНЃЌДЫЪБyЃО0ЃЌМДx2Љ2xЉ3ЃО0ЃЌЁрвЛдЊЖўДЮВЛЕШЪНx2Љ2xЉ3ЃО0ЕФНтМЏЮЊЃКxЃМЉ1ЛђxЃО3ЃЎ