题目内容
在边长为2的正三角形ABC中，已知点P是三角形内任意一点，则点P到三角形的三边距离之和PD＋PE＋PF等于（ ）
A．
B．2
C．4
D．无法确定
【答案】
A.
【解析】
试题分析：此题考查了等边三角形的性质.易利用三角形的面积求解.如图，连接AP、BP、CP，则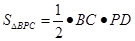
、
、
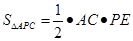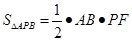；设等边三角形的高为h，由勾股定理可得：
，
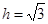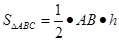.而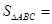
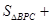
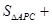
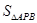，根据等边三角形三边相等，可得：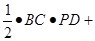
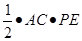
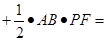
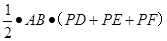
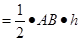，即：由此等量关系可得到三角形的三边距离之和
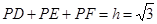.故选A.
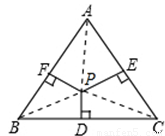
考点：等边三角形的性质.
练习册系列答案
相关题目
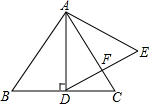如图，在边长为4的正三角形ABC中，AD⊥BC于点D，以AD为一边向右作正三角形ADE．
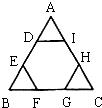18、如图，正六边形DEFGHI的顶点都在边长为6cm的正三角形ABC的边上，则这个正六边形的边长是
如图，在边长为2的正三角形ABC中，已知点P是三角形内任意一点，则点P到三角形的三边距离之和PD+PE+PF=
15、如图所示，在边长为2的正三角形ABC中，E、F、G分别为AB、AC、BC的中点，点P为线段EF上一个动点，连接BP、GP，则△BPG的周长的最小值是
（2013•南宁）如图，在边长为2的正三角形中，将其内切圆和三个角切圆（与角两边及三角形内切圆都相切的圆）的内部挖去，则此三角形剩下部分（阴影部分）的面积为