题目内容
 (2013•南宁)如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为
(2013•南宁)如图,在边长为2的正三角形中,将其内切圆和三个角切圆(与角两边及三角形内切圆都相切的圆)的内部挖去,则此三角形剩下部分(阴影部分)的面积为| 3 |
| 4 |
| 9 |
| 3 |
| 4 |
| 9 |
分析:连接OB,以及⊙O与BC的切点,在构造的直角三角形中,通过解直角三角形易求得⊙O的半径,然后作⊙O与小圆的公切线EF,易知△BEF也是等边三角形,那么小圆的圆心也是等边△BEF的重心;由此可求得小圆的半径,即可得到四个圆的面积,从而由等边三角形的面积减去四个圆的面积和所得的差即为阴影部分的面积.
解答: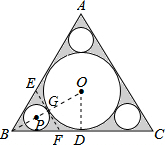 解:如图,连接OB、OD;
解:如图,连接OB、OD;
设小圆的圆心为P,⊙P与⊙O的切点为G;过G作两圆的公切线EF,交AB于E,交BC于F,
则∠BEF=∠BFE=90°-30°=60°,所以△BEF是等边三角形.
在Rt△OBD中,∠OBD=30°,
则OD=BD•tan30°=1×
=
,OB=2OD=
,BG=OB-OG=
;
由于⊙P是等边△BEF的内切圆,所以点P是△BEF的内心,也是重心,
故PG=
BG=
;
∴S⊙O=π×(
)2=
π,S⊙P=π×(
)2=
π;
∴S阴影=S△ABC-S⊙O-3S⊙P=
-
π-
π=
-
π.
故答案为
-
π.
 解:如图,连接OB、OD;
解:如图,连接OB、OD;设小圆的圆心为P,⊙P与⊙O的切点为G;过G作两圆的公切线EF,交AB于E,交BC于F,
则∠BEF=∠BFE=90°-30°=60°,所以△BEF是等边三角形.
在Rt△OBD中,∠OBD=30°,
则OD=BD•tan30°=1×
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| ||
| 3 |
由于⊙P是等边△BEF的内切圆,所以点P是△BEF的内心,也是重心,
故PG=
| 1 |
| 3 |
| ||
| 9 |
∴S⊙O=π×(
| ||
| 3 |
| 1 |
| 3 |
| ||
| 9 |
| 1 |
| 27 |
∴S阴影=S△ABC-S⊙O-3S⊙P=
| 3 |
| 1 |
| 3 |
| 1 |
| 9 |
| 3 |
| 4 |
| 9 |
故答案为
| 3 |
| 4 |
| 9 |
点评:此题主要考查了等边三角形的性质、相切两圆的性质以及图形面积的计算方法,难度适中.

练习册系列答案
相关题目
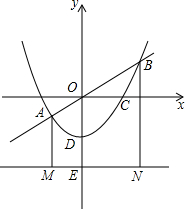 (2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N.
(2013•南宁)如图,抛物线y=ax2+c(a≠0)经过C(2,0),D(0,-1)两点,并与直线y=kx交于A、B两点,直线l过点E(0,-2)且平行于x轴,过A、B两点分别作直线l的垂线,垂足分别为点M、N. (2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=
(2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC= (2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( )
(2013•南宁)如图,圆锥形的烟囱底面半径为15cm,母线长为20cm,制作这样一个烟囱帽所需要的铁皮面积至少是( ) (2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点.
(2013•南宁)如图,在菱形ABCD中,AC为对角线,点E、F分别是边BC、AD的中点. (2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
(2013•南宁)如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.