题目内容
 如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF=
如图,在边长为2的正三角形ABC中,已知点P是三角形内任意一点,则点P到三角形的三边距离之和PD+PE+PF=分析:连接AP、BP、CP,设等边三角形的高为h,分别求出△APC、△APB、△BPC的面积,而三个三角形的面积之和等于△ABC面积,由此等量关系可求出到三角形的三边距离之和PD+PE+PF等于△ABC的高.
解答: 解:连接AP、BP、CP,设等边三角形的高为h,如图:
解:连接AP、BP、CP,设等边三角形的高为h,如图:
∵正三角形ABC边长为2
∴h=
=
∵S△BPC=
BC•PD
S△APC=
AC•PE
S△APB=
AB•PF
∴S△ABC=
BC•PD+
AC•PE+
AB•PF
∵AB=BC=AC
∴S△ABC=
BC•(PD+PE+PF)=
BC•h
∴PD+PF+PE=h=
,
故答案为
.
 解:连接AP、BP、CP,设等边三角形的高为h,如图:
解:连接AP、BP、CP,设等边三角形的高为h,如图:∵正三角形ABC边长为2
∴h=
| 22-12 |
| 3 |
∵S△BPC=
| 1 |
| 2 |
S△APC=
| 1 |
| 2 |
S△APB=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=BC=AC
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴PD+PF+PE=h=
| 3 |
故答案为
| 3 |
点评:此题考查了等边三角形的性质及三角形的面积公式,难度较大,注意计算正确.

练习册系列答案
相关题目
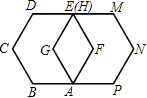 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.