Question

（本题满分8分）如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在BC边上，且∠GDF=∠ADF.

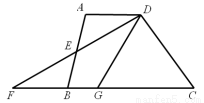
（1）求证：△ADE≌△BFE；

（2）连接EG，判断EG与DF的位置关系，并说明理由.

Answer 1

（1）详见解析；（2）EG⊥DF，理由详见解析.

【解析】

试题分析：（1）由题意可知，∠ADE=∠BFE，AE=BE，∠AED=∠BEF，满足三角形全等的条件，从而证得△ADE≌△BFE；

（2）通过证明△ADE≌△BFE，得到DE=EF，利用等腰三角形的三线合一得到EG⊥DF.

试题解析：【解析】
（1）证明：∵AD∥BC，

∴∠ADE=∠BFE（两直线平行，内错角相等），

∵E是AB的中点，

∴AE=BE，

又∵∠AED=∠BEF，

∴△ADE≌△BFE（AAS）.

（2）EG与DF的位置关系是EG⊥DF.理由如下：

∵∠ADE=∠BFE，∠GDF=∠ADF，

∴∠GDF=∠BFE（等量代换），

∴GD=GF（等角对等边），

又∵△ADE≌△BFE，

∴DE=EF（全等三角形对应边相等），

∴EG⊥DF（等腰三角形三线合一）.

考点：1、全等三角形的判定和性质；2、等腰三角形的三线合一.