题目内容
如图,一次函数 (m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.

(1)用含m的代数式分别表示点B,点E的坐标;
(2)若△ABC中AC边上的高为5,求m的值;
(3)若点P为线段AC中点,是否存在m的值,使△APD与△ABD相似?若存在,请求出m的值;若不存在,请说明理由.
 (m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(m<0)的图象经过定点A,与x轴交于点B,与y轴交于点E,AD⊥y轴于点D,将射线AB沿直线AD翻折,交y轴于点C.
(1)用含m的代数式分别表示点B,点E的坐标;
(2)若△ABC中AC边上的高为5,求m的值;
(3)若点P为线段AC中点,是否存在m的值,使△APD与△ABD相似?若存在,请求出m的值;若不存在,请说明理由.
(1)B( ,0),E(0,
,0),E(0, )(2)
)(2) (3)存在m的值,使△APD与△ABD相似,m的值为
(3)存在m的值,使△APD与△ABD相似,m的值为 或
或 或
或
 ,0),E(0,
,0),E(0, )(2)
)(2) (3)存在m的值,使△APD与△ABD相似,m的值为
(3)存在m的值,使△APD与△ABD相似,m的值为 或
或 或
或
试题分析:(1)当y=0时,
 ,∴
,∴ ,∴B(
,∴B( ,0)
,0)当x=0时,y=
 ,∴E(0,
,∴E(0, ).
). (2)由直线
 经过定点A,∴定点A(-4,3).
经过定点A,∴定点A(-4,3). 又∵AD⊥y轴,∴D(0,3).
由翻折可知:CD=ED=
 =
= ,
,∴CE=2CD=
 .
. 当点B在原点右边时,
S△ABC= S△ACE+ S△BCE=

=
 =
= =12.
=12.当点B在原点左边时,
S△ABC= S△ACE-S△BCE=
 =
= =12.
=12.∴S△ABC=12是不变化的.
∵AC边上的高为5,
∴
 =12,∴AC=
=12,∴AC= .
. ∵AD=4,∠ADC=90°,CD=
 ,
,∴
 ,解得
,解得 ,
,又∵m<0,∴
 .
. (3)存在m的值,使△APD与△ABD相似.
①当点B在原点右边时,
只有△APD∽△ADB一种情形.
由AP=PD可得AD=DB=4.
∵OD=3,∴OB=
 ,∴
,∴ =
= ,解得
,解得  .
.②当点B在原点左边时,
若△APD∽△ABD时,AB=DB,∴
 =-2,解得
=-2,解得  .
.若△APD∽△ADB时,AD=DB=4,
∵OD=3,∴OB=
 ,∴
,∴ =-
=- ,解得
,解得  .
.∴存在m的值,使△APD与△ABD相似,
m的值为
 或
或 或
或 .
. 点评:本题考查一次函数,相似三角形,解答本题需要考生掌握一次函数的概念和性质,熟悉相似三角形的判定方法,会证明两个三角形相似

练习册系列答案
相关题目

 中,
中, ,
, ,点
,点 在边
在边 上的,过点
上的,过点 ,交
,交 边于
边于 点,再把
点,再把 沿
沿 对折,点
对折,点 的对应点
的对应点 恰好落在
恰好落在 边上,则CP= .
边上,则CP= .
 . 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.
. 过点A作BC的平行线与∠ABC的平分线交于点D,连接CD. 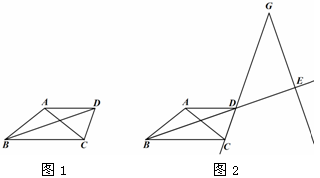
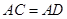 ;
; 为线段
为线段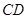 延长线上一点,将射线GC绕着点G逆时针旋转
延长线上一点,将射线GC绕着点G逆时针旋转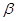 ,与射线BD交于点E.
,与射线BD交于点E. ,
, ,如图2所示,求证:
,如图2所示,求证: ;
; ,
, ,请直接写出
,请直接写出 的值(用含
的值(用含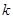 的代数式表示).
的代数式表示).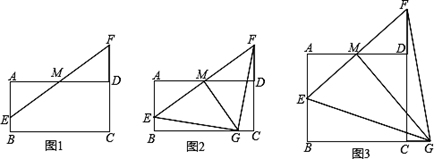
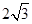 ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.