题目内容
13.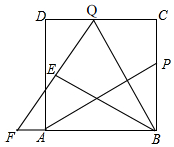 如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长;
(3)若BP=2PC,求QF的长.
分析 (1)证明△ABP≌△BCQ,则∠BAP=∠CBQ,从而证明∠CBQ+∠APB=90°,进而得证;
(2)先由折叠得出∠CBQ=∠EBQ,再由垂直平分线得出∠EBQ=∠EBF,即可得出∠CBQ=30°,即可得出结论.
(3)设FQ=FB=x,则FE=x-4.在直角△FBE中,利用勾股定理即可列方程求解;
解答 解:(1)AP⊥BQ
理由:∵四边形ABCD是正方形,
∴∠ABC=∠C=90°,AB=BC.
∴在△ABP和△BCQ中,$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠C}\\{BP=CQ}\end{array}\right.$,
∴△ABP≌△BCQ,
∴∠BAP=∠CBQ.
∵∠BAP+∠APB=90°,
∴∠CBQ+∠APB=90°,
∴∠BEP=90°,
∴AP⊥BQ;
(2)∵将△BQC沿BQ所在的直线翻折得到△BQE,
∴∠CBQ=∠EBQ,∠QEB=∠FEB=90°,
∵E是FQ的中点,
∴QE=FE,
∴∠QBE=∠FBE,
∴∠CBQ=∠EBQ=∠FBQ=$\frac{1}{3}$∠ABC=30°,
在Rt△BCQ中,tan∠CBQ=tan30°=$\frac{CQ}{BC}$,
∴$\frac{\sqrt{3}}{3}=\frac{CQ}{6}$,
∴CQ=2$\sqrt{3}$,
由(1)知,△ABP≌△BCQ,
∴BP=CQ=2$\sqrt{3}$;
(3)由(1)可得EQ=CQ=BP=4,EB=BC=6.
又∵∠EQB=∠CQB=∠ABQ,
∴FQ=FB.
设FQ=FB=x,则FE=x-4.
在Rt△FBE中,FB2=BE2+FE2,
即x2=62+(x-4)2,
解得:x=$\frac{13}{2}$,
即FQ=$\frac{13}{2}$;
点评 此题是四边形综合题,主要考查正方形的性质,折叠的性质,全等三角形的判定,勾股定理,锐角三角函数,判断出FQ=FB是解本题的关键,利用直角三角形是解这类题目的关键.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案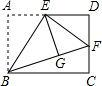 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=$\sqrt{96}$,则DF的长为 ( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | $2\sqrt{3}$ |
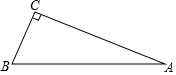 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,则∠A的正弦值为( )| A. | $\frac{5}{12}$ | B. | $\frac{12}{13}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{13}$ |

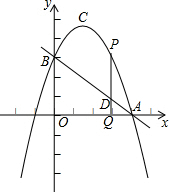 如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.
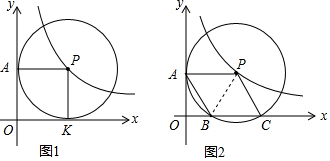
如图,抛物线顶点坐标为点C(2,8),交x轴于点A (6,0),交y轴于点B.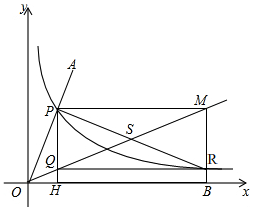 如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.
如图,在平面直角坐标系中,射线OA交反比例函数y=$\frac{1}{x}$(x>0)图象于点P,点R为反比例函数y=$\frac{1}{x}$(x>0)图象上的另一点,且PR=2OP,分别过点P、R作x轴、y轴的平行线,两线相交于点M(a,b),直线MR交x轴于点B,过点P作y轴的平行线分别交直线OM和x轴于点Q、H,连接RQ.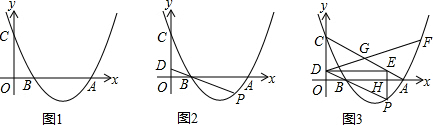
 如图:函数y1=$\frac{1}{2}$x-2和y=-3x+5交于点A(2,-1),当x<2 时y1<y2.
如图:函数y1=$\frac{1}{2}$x-2和y=-3x+5交于点A(2,-1),当x<2 时y1<y2.