Question

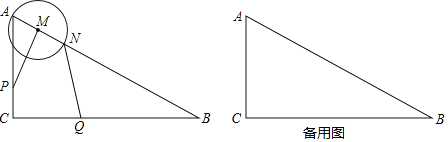
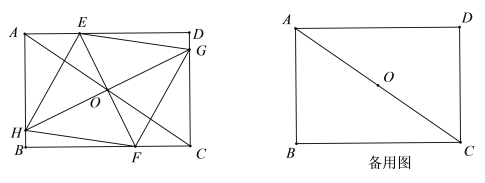
【题目】如图，已知在平行四边形ABCD中，AB＝10，BC＝15，tan∠A＝，点P是边AD上一点，联结PB，将线段PB绕着点P逆时针旋转90°得到线段PQ，如果点Q恰好落在平行四边形ABCD的边上，那么AP的值是_____．

Answer 1

【答案】6或10

【解析】

分情况解答：当点Q落在CD上时，作BE⊥AD于E，QF⊥AD交AD的延长线于F．设PE＝x，通过证明△PBE≌△QPF，得出PE＝QF＝x，DF＝x﹣1，由tan∠FDQ＝tanA＝＝，即可得出AP的值；当点Q落在AD上时，得出∠APB＝∠BPQ＝90°，由tanA＝，即可得出AP的值；当点Q落在直线BC上时，作BE⊥AD于E，PF⊥BC于F．则四边形BEPF是矩形．由tanA＝＝，可得出△BPQ是等腰直角三角形，此时求出BQ不满足题意，舍去.

解：如图1中，当点Q落在CD上时，作BE⊥AD于E，QF⊥AD交AD的延长线于F．

设PE＝x．

在Rt△AEB中，∵tanA＝＝，AB＝10，

∴BE＝8，AE＝6，

∵将线段PB绕着点P逆时针旋转90°得到线段PQ，

∴∠BPQ＝90°，

∴∠EBP+∠BPE＝∠BPE+∠FPQ＝90°，

∴∠EBP＝∠FPQ，

∵PB＝PQ，∠PEB＝∠PFQ＝90°，

∴△PBE≌△QPF（AAS），

∴PE＝QF＝x，EB＝PF＝8，

∴DF＝AE+PE+PF﹣AD＝x﹣1，

∵CD∥AB，

∴∠FDQ＝∠A，

∴tan∠FDQ＝tanA＝＝，

∴＝，

∴x＝4，

∴PE＝4，

∴AP＝6+4＝10；

如图2，当点Q落在AD上时，

∵将线段PB绕着点P逆时针旋转90°得到线段PQ，

∴∠BPQ＝90°，

∴∠APB＝∠BPQ＝90°，

在Rt△APB中，∵tanA＝＝，AB＝10，

∴AP＝6；

如图3中，当点Q落在直线BC上时，作BE⊥AD于E，PF⊥BC于F．则四边形BEPF是矩形．

在Rt△AEB中，∵tanA＝＝，AB＝10，

∴BE＝8，AE＝6，

∴PF＝BE＝8，

∵△BPQ是等腰直角三角形，PF⊥BQ，

∴PF＝BF＝FQ＝8，

∴PB＝PQ＝8，BQ＝PB＝16＞15（不合题意舍去），

综上所述，AP的值是6或10，

故答案为：6或10．