Question

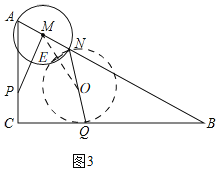
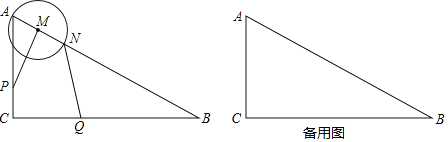
【题目】如图，已知在△ABC中，∠ACB＝90°，AC＝4，BC＝8，点P是射线AC上一点（不与点A、C重合），过P作PM⊥AB，垂足为点M，以M为圆心，MA长为半径的⊙M与边AB相交的另一个交点为点N，点Q是边BC上一点，且CQ＝2CP，联结NQ．

（1）如果⊙M与直线BC相切，求⊙M的半径长；

（2）如果点P在线段AC上，设线段AP＝x，线段NQ＝y，求y关于x的函数解析式及定义域；

（3）如果以NQ为直径的⊙O与⊙M的公共弦所在直线恰好经过点P，求线段AP的长．

Answer 1

【答案】（1）；（2）（0＜x＜4）；（3）或．

【解析】

（1）先根据勾股定理求得，设⊙M的半径长为R，则，过M作MH⊥BC，垂足为点H，根据相似三角形的对应边成比例得到，最后根据⊙M与直线BC相切，即MA＝MH，即可求解；

（2）设AP＝x，得到CP＝4﹣x，CQ＝8﹣2x，BQ＝2x，过Q作QG⊥AB，垂足为点G，根据三角函数可得，根据PM⊥AB，，得到，最后在Rt△QNG中，根据勾股定理即可求解；

（3）当点P在线段AC上，设以NQ为直径的⊙O与⊙M的另一个交点为点E，连接EN，MO，则MO⊥EN，根据以NQ为直径的⊙O与⊙M的公共弦所在直线恰好经过点P，PM⊥AB，MA＝MN，得到PN＝PA，∠PAN＝∠ANE，再根据∠ACB＝90°，得到∠PAN+∠B＝90°，∠NMO＝∠B，连接AQ，根据 M、O分别是线段AN、NQ的中点，得到MO∥AQ，∠NMO＝∠BAQ，∠BAQ＝∠B， QA＝QB，在Rt△QAC中，根据勾股定理得，QA2＝AC2+QC2即可求解；当点P在线段AC的延长上，即．

（1）解：如图1，

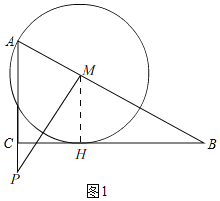
在Rt△ABC中，

∵∠ACB＝90°，AC＝4，BC＝8，

∴

设⊙M的半径长为R，则

过M作MH⊥BC，垂足为点H，

∴MH∥AC，

∵MH∥AC，

∴△BHM∽△BCA，

∴

∵⊙M与直线BC相切，

∴MA＝MH，

∴

∴，

即的半径长为；

（2）如图2，

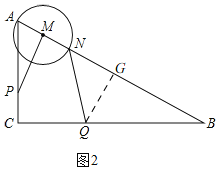
∵AP＝x，

∴CP＝4﹣x，

∵CQ＝2CP，

∴CQ＝8﹣2x，

∴BQ＝BC﹣CQ＝8﹣（8﹣2x）＝2x，

过Q作QG⊥AB，垂足为点G，

∵，

∴，

∴

同理：

∵PM⊥AB，

∴∠AMP＝90°，

∴

∵AP＝x，

∴

∴

在Rt△QNG中，根据勾股定理得，QN2＝NG2+QG2，

∴

∴（0＜x＜4）；

（3）当点P在线段AC上，如图3，

设以NQ为直径的⊙O与⊙M的另一个交点为点E，连接EN，MO，

则MO⊥EN，

∴∠NMO+∠ANE＝90°，

∵以NQ为直径的⊙O与⊙M的公共弦所在直线恰好经过点P，

即P、E、N在同一直线上，

又∵PM⊥AB，MA＝MN，

∴PN＝PA，

∴∠PAN＝∠ANE，

∵∠ACB＝90°，

∴∠PAN+∠B＝90°，

∴∠NMO＝∠B，

连接AQ，

∵M、O分别是线段AN、NQ的中点，

∴MO∥AQ，

∴∠NMO＝∠BAQ，

∴∠BAQ＝∠B，

∴QA＝QB，

在Rt△QAC中，根据勾股定理得，QA2＝AC2+QC2，

∴（2x）2＝42+（8﹣2x）2，

∴

同理：当点P在线段AC的延长上，

即线段AP的长为或．