题目内容
5.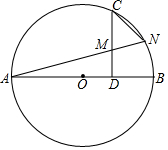 如图在⊙O中,AB为直径,过OB的中点D作CD⊥AB交⊙O于C,M为CD的中点,且CD=$\sqrt{3}$,连接AM并延长交⊙O于N.
如图在⊙O中,AB为直径,过OB的中点D作CD⊥AB交⊙O于C,M为CD的中点,且CD=$\sqrt{3}$,连接AM并延长交⊙O于N.(1)求∠ANC的大小;
(2)求弦CN的长.
分析 (1)连接OC,根据已知条件得到OD=$\frac{1}{2}$OB=$\frac{1}{2}$OC,根据三角形的内角和得到∠COD=60°,由邻补角的定义得到∠AOC=120°,于是得到∠ANC=$\frac{1}{2}$∠AOC=60°,;
(2)连接AC,由的第三轮得到OC=$\sqrt{O{D}^{2}+C{D}^{2}}$=2,AM=$\sqrt{A{D}^{2}+D{M}^{2}}$=$\sqrt{10}$,根据相似三角形的性质即可得到结论.
解答  解:(1)连接OC,
解:(1)连接OC,
则OC=OB,
∵D是OB的中点,
∴OD=$\frac{1}{2}$OB=$\frac{1}{2}$OC,
∵CD⊥AB,
∴∠CDO=90°,
∴∠OCD=30°,
∴∠COD=60°,
∴∠AOC=120°,
∴∠ANC=$\frac{1}{2}$∠AOC=60°,;
(2)连接AC,
∴OC=$\sqrt{O{D}^{2}+C{D}^{2}}$=2,
∴OD=1,
∴AD=3,
∴AC=2$\sqrt{3}$,
∴AM=$\sqrt{A{D}^{2}+D{M}^{2}}$=$\sqrt{10}$,
∵∠CAO=∠ACO=30°,
∴∠ACD=60°,
∴∠ACD=∠N,
∵∠CAM=∠NAC,
∴△ACM∽△ANC,
∴$\frac{AC}{AM}$=$\frac{CN}{CM}$,即$\frac{2\sqrt{3}}{\sqrt{10}}$=$\frac{CN}{1}$,
∴CN=$\frac{\sqrt{30}}{5}$.
点评 本题考查了勾股定理,解直角三角形,圆周角定理,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.计算1-(-2)的正确结果是( )
| A. | -2 | B. | -1 | C. | 1 | D. | 3 |
13.甲袋中装有形状、大小与质地都相同的红球3个,乙袋中装有形状、大小与质地都相同的红球2个,黄球1个,下列事件为随机事件的是( )
| A. | 从甲袋中随机摸出1个球,是黄球 | |
| B. | 从甲袋中随机摸出1个球,是红球 | |
| C. | 从乙袋中随机摸出1个球,是红球或黄球 | |
| D. | 从乙袋中随机摸出1个球,是黄球 |
10.方程x2=3x的解为( )
| A. | x=3 | B. | x=0 | C. | x1=0,x2=-3 | D. | x1=0,x2=3 |
17.不等式组$\left\{\begin{array}{l}{1-x≤2}\\{2x-1<3}\end{array}\right.$的解集是( )
| A. | x<2 | B. | x>-1 | C. | -1≤x<2 | D. | 1≤x<2 |
14.一艘轮船满载排水量为38000吨,把数38000用科学记数法表示为( )
| A. | 3.8×103 | B. | 38×103 | C. | 3.8×104 | D. | 3.8×105 |
15.在反比例函数y=$\frac{1-3m}{x}$图象上有两点A(x1,y1),B(x2,y2),若x1<x2<0,y1<y2,则m的取值范围是( )
| A. | m$>\frac{1}{3}$ | B. | m$<\frac{1}{3}$ | C. | m$≥\frac{1}{3}$ | D. | m$≤\frac{1}{3}$ |