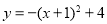题目内容
如图所示,直线l:y=3x+3与x轴交于点A,与y轴交于点B.把△AOB沿y轴翻折,点A落到点C,抛物线过点B、C和D(3,0).

(1)求直线BD和抛物线的解析式.
(2)若BD与抛物线的对称轴交于点M,点N在坐标轴上,以点N、B、D为顶点的三角形与△MCD相似,求所有满足条件的点N的坐标.
(3)在抛物线上是否存在点P,使S△PBD=6?若存在,求出点P的坐标;若不存在,说明理由.
(1)直线BD的解析式为:y=-x+3.抛物线的解析式为:y=x2-4x+3.(2)点N坐标为:(0,0),(-3,0)或(0,-3).点P的坐标为(4,3)或(-1,8).
【解析】
试题分析:(1)由待定系数法求出直线BD和抛物线的解析式;
(2)首先确定△MCD为等腰直角三角形,因为△BND与△MCD相似,所以△BND也是等腰直角三角形.如答图1所示,符合条件的点N有3个;
(3)如答图2、答图3所示,解题关键是求出△PBD面积的表达式,然后根据S△PBD=6的已知条件,列出一元二次方程求解.
试题解析:(1)∵直线l:y=3x+3与x轴交于点A,与y轴交于点B,
∴A(-1,0),B(0,3);
∵把△AOB沿y轴翻折,点A落到点C,∴C(1,0).
设直线BD的解析式为:y=kx+b,
∵点B(0,3),D(3,0)在直线BD上,
∴ ,
,
解得k=-1,b=3,
∴直线BD的解析式为:y=-x+3.
设抛物线的解析式为:y=a(x-1)(x-3),
∵点B(0,3)在抛物线上,
∴3=a×(-1)×(-3),
解得:a=1,
∴抛物线的解析式为:y=(x-1)(x-3)=x2-4x+3.
(2)抛物线的解析式为:y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1).
直线BD:y=-x+3与抛物线的对称轴交于点M,令x=2,得y=1,
∴M(2,1).
设对称轴与x轴交点为点F,则CF=FD=MF=1,
∴△MCD为等腰直角三角形.
∵以点N、B、D为顶点的三角形与△MCD相似,
∴△BND为等腰直角三角形.
如答图1所示:

(Ⅰ)若BD为斜边,则易知此时直角顶点为原点O,
∴N1(0,0);
(Ⅱ)若BD为直角边,B为直角顶点,则点N在x轴负半轴上,
∵OB=OD=ON2=3,
∴N2(-3,0);
(Ⅲ)若BD为直角边,D为直角顶点,则点N在y轴负半轴上,
∵OB=OD=ON3=3,
∴N3(0,-3).
∴满足条件的点N坐标为:(0,0),(-3,0)或(0,-3).
(3)假设存在点P,使S△PBD=6,设点P坐标为(m,n).
(Ⅰ)当点P位于直线BD上方时,如答图2所示:

过点P作PE⊥x轴于点E,则PE=n,DE=m-3.
S△PBD=S梯形PEOB-S△BOD-S△PDE= (3+n)m-
(3+n)m- ×3×3-
×3×3- (m-3)n=6,
(m-3)n=6,
化简得:m+n=7 ①,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入①式整理得:m2-3m-4=0,
解得:m1=4,m2=-1,
∴n1=3,n2=8,∴P1(4,3),P2(-1,8);
(Ⅱ)当点P位于直线BD下方时,如答图3所示:

过点P作PE⊥y轴于点E,则PE=m,OE=-n,BE=3-n.
S△PBD=S梯形PEOD+S△BOD-S△PBE= (3+m)(-n)+
(3+m)(-n)+ ×3×3-
×3×3- (3-n)m=6,
(3-n)m=6,
化简得:m+n=-1 ②,
∵P(m,n)在抛物线上,
∴n=m2-4m+3,
代入②式整理得:m2-3m+4=0,△=-7<0,此方程无解.
故此时点P不存在.
综上所述,在抛物线上存在点P,使S△PBD=6,点P的坐标为(4,3)或(-1,8).
考点:二次函数综合题.

 根据上述算
根据上述算 B.
B. C.
C. D.
D.






 ,则
,则 ( )
( ) B、
B、 C、
C、 D、
D、
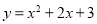 绕着它与
绕着它与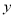 轴的交点旋转180°,所得抛物线的解析式是( ).
轴的交点旋转180°,所得抛物线的解析式是( ).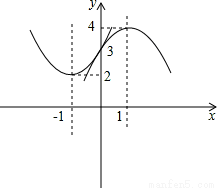
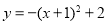 B.
B.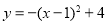
 D.
D.