题目内容
要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.  x(x+1)=28 B.
x(x+1)=28 B.  x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
已知x1、x2是一元二次方程x2﹣4x+1=0的两个根,则x1+x2等于( )
A.﹣4 B.﹣1 C.1 D.4
查看答案抛物线y=2x2-3的顶点在( )
A. 第一象限 B. 第二象限 C. x轴上 D. y轴
查看答案下列函数解析式中,一定为二次函数的是()
A. y=3x?1 B. y=ax2+bx+c
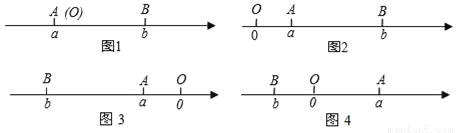
C. s=2t2+2t+1 D. y=x2+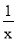
一元二次方程x2﹣2x=0的根是( )
A. x1=0,x2=﹣2 B. x1=1,x2=2 C. x1=1,x2=﹣2 D. x1=0,x2=2
查看答案阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
查看答案 试题属性- 题型:单选题
- 难度:简单
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
用小棋子摆出如下图形,则第n个图形中小棋子的个数为( )
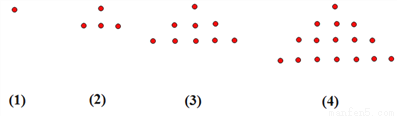
A. n B. 2n C. n2 D. n2+1
C 【解析】∵第一个图棋子数目为1=12, 第二个图棋子数目为1+3=4=22, 第三个图棋子数目为1+3+5=9=32, 第四个图棋子数目为1+3+5+7=16=42, … ∴第n个图棋子数目为n2枚。 故选:C.某市居民用电的电价实行阶梯收费,收费标准如下表:
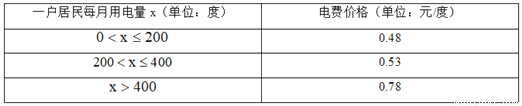
七月份是用电高峰期,李叔计划七月份电费支出不超过200元,直接写出李叔家七月份最多可用电的度数是( )
A. 100 B. 396 C. 397 D. 400
查看答案将直尺和直角三角板按如图方式摆放(∠ACB为直角),已知∠1=30°,则∠2的大小是( )
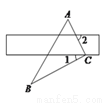
A. 30° B. 45° C. 60° D. 65°
查看答案小文统计了本班同学一周的体育锻练情况,并绘制了直方图
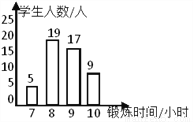
①小文同学一共统计了60人;
②这个班同学一周参加体育锻炼时间的众数是8;
③这个班同学一周参加体育锻炼时间的中位数是9;
④这个班同学一周参加体育锻炼时间的平均值为8.
根据图中信息,上述说法中正确的是( )
A. ①② B. ②③ C. ③④ D. ①④
查看答案下列因式分解正确的是( )
A. 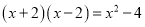 B.
B. 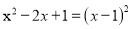
C. 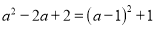 D.
D. 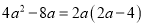
若把不等式x+2≤0的解集在数轴上表示出来,则正确的是( )
A.  B.
B. 
C. 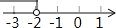 D.
D. 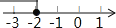
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
用适当的方法解下列方程.
①(2x+3)2﹣16=0;
②2x2=3(2x+1).
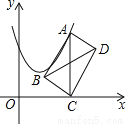
【解析】 ①∴x1=,x2=﹣;②∴x1=,x2=. 【解析】试题分析:先观察方程,再确定各方程的解法;①用直接开平方法,②根据题意用公式法求解.需注意②先要将方程化为一般式. 试题解析:【解析】 ①(2x+3)2﹣16=0, ∴(2x+3)2=16, ∴2x+3=±4, ∴x1=,x2=﹣; ②2x2=3(2x+1), 原方程可化为:2x2﹣6x﹣3...如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+4上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为____.
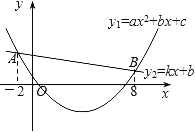
已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+b(k≠0)的图象相交于点A(﹣2,4),B(8,2)(如图所示),则能使y1>y2成立的x的取值范围是 .
某药品原价每盒25元,为了响应国家解决老百姓看病贵的号召,经过连续两次降价,现在售价每盒16元,则该药品平均每次降价的百分率是_____%.
查看答案已知抛物线y=ax2-3x+c(a≠0)经过点(-2,4),则4a+c-1=____.
查看答案若一元二次方程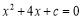 有两个不相等的实数根,则c的值可以是 (写出一个即可).
有两个不相等的实数根,则c的值可以是 (写出一个即可).
- 题型:解答题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
如图是二次函数y=ax2+bx+c过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac,②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( )
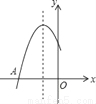
A. ②④ B. ①④ C. ②③ D. ①③
B 【解析】试题分析:由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上得到c>0,由对称轴为x==-1可以判定②错误;由图象与x轴有交点,对称轴为x==-1,与y轴的交点在y轴的正半轴上,可以推出b2-4ac>0,即b2>4ac,①正确;由x=-1时y有最大值,由图象可知y≠0,③错误.然后即可作出选择. 故选B.设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
查看答案在同一坐标系中,一次函数y=-mx+n2与二次函数y=x2+m的图象可能是( )
A.  B.
B.  C.
C.  D.
D. 
关于x的一元二次方程x2﹣3x+m=0没有实数根,则实数m的取值范围为( )
A.  B.
B.  C.
C.  D.
D. 
抛物线y=3x2+2x-1向上平移4个单位长度后的函数解析式为( )
A. y=3x2+2x-5 B. y=3x2+2x-4 C. y=3x2+2x+3 D. y=3x2+2x+4
查看答案要组织一次排球邀请赛,参赛的每两个队之间都要比赛一场,根据时间和场地等条件,赛程计划安排7天,每天安排4场比赛,设比赛组织者应邀请x个队参赛,则x满足的关系式为( )
A.  x(x+1)=28 B.
x(x+1)=28 B.  x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
x(x-1)=28 C. x(x+1)=28 D. x(x-1)=28
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
阅读下面材料:已知点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为|AB|,当A、B两点中有一点在原点时,不妨设点A在原点,如图1,|AB|=|OB|=|b|=|a﹣b|,当A、B两点都不在原点时.
(1)如图2,点A、B都在原点的右边,|AB|=|OB|﹣|OA|=|b|﹣|a|=b﹣a=|a﹣b|
(2)如图3,点A、B都在原点的左边,|AB|=|OB|﹣|OA|=|b|﹣|a|=﹣b﹣(﹣a)=a﹣b=|a﹣b|
(3)如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(﹣b)=a﹣b=|a﹣b|
综上,数轴上A、B两点的距离|AB|=|a﹣b|

回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ,数轴上表示﹣2和﹣5的两点之间的距离是 ,数轴上表示﹣2和5的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点A和B之间的距离是 ,如果|AB|=2那么x为 .
(3)若x表示一个有理数,则|x﹣1|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
(1)3;3;7;(2)|x+1|,1或﹣3;(3)4. 【解析】试题分析:(1)数轴上表示2和5的两点之间的距离是|5-2|=3,-2和-5的两点之间的距离是|-2-(-5)|=3,表示-2和5的两点之间的距离是|5-(-2)|=7;(2)数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,令|x+1|=2,解得x=1或-3;(3)代数式|x-1|+|x+3|表示数轴上...甲、乙两家商场以同样的价格出售同样的电器,但各自推出的优惠方案不同.甲商场规定:凡超过1000元的电器,超出的金额按90%收取;乙商场规定:凡超过500元的电器,超出的金额按95%收取.某顾客购买的电器价格是x元.
(1)当x=850时,该顾客应选择在 商场购买比较合算;
(2)当x>1000时,分别用代数式表示在两家商场购买电器所需付的费用;
(3)当x=1700时,该顾客应选择哪一家商场购买比较合算?说明理由.
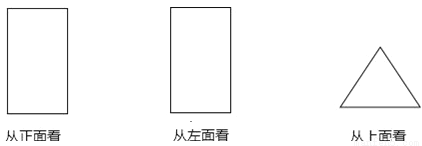
查看答案已知如图为一几何体的三种形状图:
(1)这个几何体的名称为 ;
(2)任意画出它的一种表面展开图;
(3)若从正面看到的是长方形,其长为10cm;从上面看到的是等边三角形,其边长为4cm,求这个几何体的侧面积.
司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自A地出发到收工时,行走记录为(单位:千米):+8、﹣9、+7、﹣2、+5、﹣10、+7、﹣3,回答下列问题
(1)收工时小王在A地的哪边?距A地多少千米?
(2)若每千米耗油0.2升,问从A地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离A地多远?
查看答案化简与求值:
(1)化简: 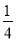 (﹣4x2+2x﹣8)﹣(
(﹣4x2+2x﹣8)﹣(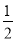 x﹣1)
x﹣1)
(2)先化简,再求值:2(a2b+ab2)﹣2(a2b﹣1)﹣2ab2﹣2,其中a=﹣2,b=2.
查看答案计算:
(1)16÷(﹣23)﹣(﹣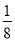 )×(﹣4)
)×(﹣4)
(2)﹣4﹣(﹣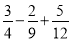 )÷
)÷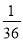
(3)﹣14﹣[2﹣(﹣3)2]÷(﹣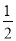 )3.
)3.
- 题型:解答题
- 难度:困难
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
小明与小刚规定了一种新运算*:若a、b是有理数,则a*b=3a﹣2b.小明计算出2*5=﹣4,请你帮小刚计算2*(﹣5)=_____.
16 【解析】试题解析:根据题中的新定义得:2*(-5)=3×2-2×(-5)=6+10=16.若x2+x=2,则(x2+2x)﹣(x+1)值是_____.
查看答案如果(x+3)2+|y﹣2|=0,则xy=_____.
查看答案如图所示的运算程序中,若开始输入的x值为48,我们发现第1次输出的结果为24,第2次输出的结果为12,…第2017次输出的结果为( )
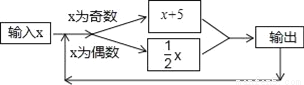
A. 3 B. 6 C. 4 D. 2
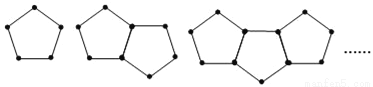
查看答案下列是由一些火柴搭成的图案:图①用了5根火柴,图②用了9根火柴,图③用了13根火柴,按照这种方式摆下去,摆第5个图案用多少根火柴棒( )
A. 20 B. 21 C. 22 D. 23
查看答案多项式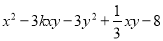 合并同类项后不含xy项,则k的值是( )
合并同类项后不含xy项,则k的值是( )
A. 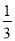 B.
B. 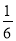 C.
C. 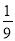 D. 0
D. 0
- 题型:填空题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
下面几何体的截面图可能是圆的是( )
A. 正方体 B. 圆锥 C. 长方体 D. 棱柱
B 【解析】试题分析:截面可能为圆的图形,原图形中必须含有圆的因数,本题中A、C、D选项中均不含有.﹣2017的相反数是( )
A. ﹣2017 B. 2017 C. ±2017 D. 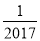
如图,半圆O的直径MN=6cm,在△ABC中,∠ACB=90°,∠ABC=30°,BC=6cm,半圆O以1cm/s的速度从左向右运动,在运动过程中,点M、N始终在直线BC上,设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=4cm.
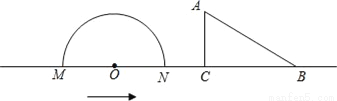
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在圆相切时,如果半圆O与直线MN围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积.
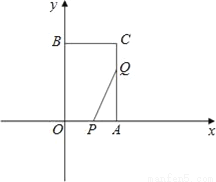
查看答案如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm2?
(2)△PAQ的面积能否达到3cm2?
(3)经过多长时间,P、Q两点之间的距离为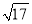 cm?
cm?
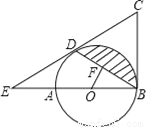
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案 试题属性- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
某种品牌的彩电降价30%以后,每台售价为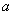 元,则该品牌彩电每台原价应为( )
元,则该品牌彩电每台原价应为( )
A. 0.7a元 B. 0.3a元 C. 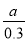 元 D.
元 D. 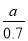 元
元
用四舍五入法按要求对0.05019分别取近似值,其中错误的是( )
A. 0.1(精确到0.1) B. 0.05(精确到千分位)
C. 0.05(精确到百分位) D. 0.0502(精确到0.0001)
查看答案下列各式计算中,正确的是( )
A. 2a+2=4a B. ﹣2x2+4x2=2x2 C. x+x=x2 D. 2a+3b=5ab
查看答案下列说法正确的是( )
A. 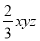 与
与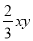 是同类项 B.
是同类项 B. 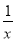 和
和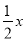 是同类项
是同类项
C. 0.5x3y2与7x2y3是同类项 D. 5m2n与﹣4nm2是同类项
查看答案下列各式中,等号不成立的是( )
A. |﹣4|=4 B. ﹣|4|=|﹣4| C. |﹣4|=|4| D. ﹣|﹣4|=﹣4
查看答案下列式子中,正确的是( )
A. ﹣6<﹣8 B. ﹣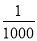 >0 C. ﹣
>0 C. ﹣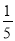 <﹣
<﹣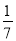 D.
D. 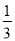 <0.3
<0.3
- 题型:单选题
- 难度:中等
 Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧


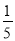 a2b D. 52与25
a2b D. 52与25