题目内容
6.已知等腰三角形的两边长分别为方程组$\left\{\begin{array}{l}{\sqrt{5}x+\sqrt{3}y=4}\\{\sqrt{5}x-\sqrt{3}y=1}\end{array}\right.$的两个根,求这个等腰三角形的面积.分析 通过解方程组结合三角形的三边关系可得出等腰三角形的三条边分别为:$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{5}}{2}$或$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{5}}{2}$,$\frac{\sqrt{5}}{2}$,再利用勾股定理以及等腰三角形的性质可求出底边上的高,利用三角形的面积公式即可得出结论.
解答 解:方程组$\left\{\begin{array}{l}{\sqrt{5}x+\sqrt{3}y=4}\\{\sqrt{5}x-\sqrt{3}y=1}\end{array}\right.$的解为:$\left\{\begin{array}{l}{x=\frac{\sqrt{5}}{2}}\\{y=\frac{\sqrt{3}}{2}}\end{array}\right.$,
根据三角形的三边关系可知,等腰三角形的三条边分别为:$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{5}}{2}$或$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{5}}{2}$,$\frac{\sqrt{5}}{2}$.
当腰为$\frac{\sqrt{3}}{2}$时,AB=$\frac{\sqrt{3}}{2}$,BD=$\frac{\sqrt{5}}{4}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\frac{\sqrt{7}}{4}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×$\frac{\sqrt{5}}{2}$×$\frac{\sqrt{7}}{4}$=$\frac{\sqrt{35}}{16}$;
当腰为$\frac{\sqrt{5}}{2}$时,AB=$\frac{\sqrt{5}}{2}$,BD=$\frac{\sqrt{3}}{4}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\frac{\sqrt{17}}{4}$,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{17}}{4}$=$\frac{\sqrt{51}}{16}$.
故这个等腰三角形的面积为$\frac{\sqrt{35}}{16}$或$\frac{\sqrt{51}}{16}$.
点评 本题考查了二次根式的应用、解二元一次方程组、等腰三角形的性质、三角形的三边关系、勾股定理以及三角形的面积,利用三角形的三边关系确定等腰三角形的三条边长是解题的关键.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| (x,y) | (n,n) | (m,n) | (n,m) |
| f(x,y) | n | m-n | m+n |
| A. | 5 | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | -5 |
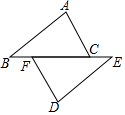 如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )
如图,点B、F、C、E在一条直线上,AB∥ED,AB=DE,要使△ABC≌△DEF,需要添加下列选项中的一个条件是( )| A. | BF=EC | B. | AC=DF | C. | ∠B=∠E | D. | BF=FC |
 如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )
如图,在△ABC中,DE∥BC,分别交AB,AC于点D,E.若AD=1,DB=2,则△ADE的面积与△ABC的面积的比等于( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{9}$ |