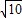题目内容
在△ABC中,最大角∠A是最小角∠C的两倍,且AB=6,AC=8,则BC=________.
2
分析:作出∠A的平分线AD,利用相似三角形的判定得出△BAD∽△BCA,进而得出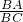 =
= =
= ,从而得出48=AD•BC,6AD=8(BC-AD),进而得出BC的值.
,从而得出48=AD•BC,6AD=8(BC-AD),进而得出BC的值.
解答: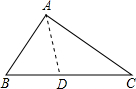 解:方法一:作∠A的平分线AD,
解:方法一:作∠A的平分线AD,
∵最大角∠A是最小角∠C的两倍,
∴∠BAD=∠DAC=∠DAC,
∴AD=CD,
∵∠BAC=2∠C,
∴∠BAD=∠C,
又∵∠B=∠B,
∴△BAD∽△BCA,
∴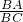 =
= =
= ,
,
∴ =
= =
=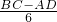 ,
,
∴48=AD•BC,6AD=8(BC-AD),
解得:BC= AD,
AD,
∴CB= =2
=2 .
.
故答案为:2 .
.
方法二:解:假设∠C=x,
∴∠A=2x,
∴∠B=180-3x,
∵sin3x=sin(180-3x),
∵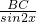 =
=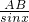 =
=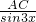 ,
,
∴BCsin3x=8sin2x,
∴BCsinx=6sin2x,
∴BC=12cosx,
∴sin3x= sinx,
sinx,
∴3sinx-4sinx3= sinx,
sinx,
4sinx2=3- =
= ,sinx=
,sinx= ,cosx=
,cosx=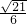 ,
,
BC=12×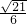 =2
=2 .
.
故答案为:2 .
.
点评:此题主要考查了相似三角形的判定与性质,作出辅助线后利用相似三角形性质求出是解决问题的关键.

分析:作出∠A的平分线AD,利用相似三角形的判定得出△BAD∽△BCA,进而得出
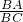 =
= =
= ,从而得出48=AD•BC,6AD=8(BC-AD),进而得出BC的值.
,从而得出48=AD•BC,6AD=8(BC-AD),进而得出BC的值.解答:
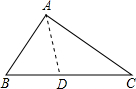 解:方法一:作∠A的平分线AD,
解:方法一:作∠A的平分线AD,∵最大角∠A是最小角∠C的两倍,
∴∠BAD=∠DAC=∠DAC,
∴AD=CD,
∵∠BAC=2∠C,
∴∠BAD=∠C,
又∵∠B=∠B,
∴△BAD∽△BCA,
∴
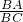 =
= =
= ,
,∴
 =
= =
=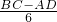 ,
,∴48=AD•BC,6AD=8(BC-AD),
解得:BC=
 AD,
AD,∴CB=
 =2
=2 .
.故答案为:2
 .
.方法二:解:假设∠C=x,
∴∠A=2x,
∴∠B=180-3x,
∵sin3x=sin(180-3x),
∵
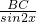 =
=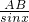 =
=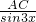 ,
,∴BCsin3x=8sin2x,
∴BCsinx=6sin2x,
∴BC=12cosx,
∴sin3x=
 sinx,
sinx,∴3sinx-4sinx3=
 sinx,
sinx,4sinx2=3-
 =
= ,sinx=
,sinx= ,cosx=
,cosx=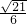 ,
,BC=12×
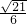 =2
=2 .
.故答案为:2
 .
.点评:此题主要考查了相似三角形的判定与性质,作出辅助线后利用相似三角形性质求出是解决问题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目


 -
-